1 Funktionsweise
Erstellt: DL6GL, 29.09.2014, letzte Änderung
| « Armeleute-DDS-Funktionsgenerator | TOP | » 2 Schaltung |
Wenn die Software schon da ist, wäre es mal eine Überlegung wert, warum sie so funktioniert wie sie funktioniert. Die integrierten DDS machen es nicht anders, wenn auch unsichtbar im Chip. Sie erzeugen aus einer digitalen Bitfolge, was nichts anderes als eine bestimmte Zahl ist, ein fast analoges, d.h. treppenförmiges Ausgangssignal. Bei der Zu-Fuß-Lösung mit einer diskreten R2R-Kette wird ein 8 Bit breiter AVR-Port zur Ansteuerung verwendet.
1.1 R2R-DAC
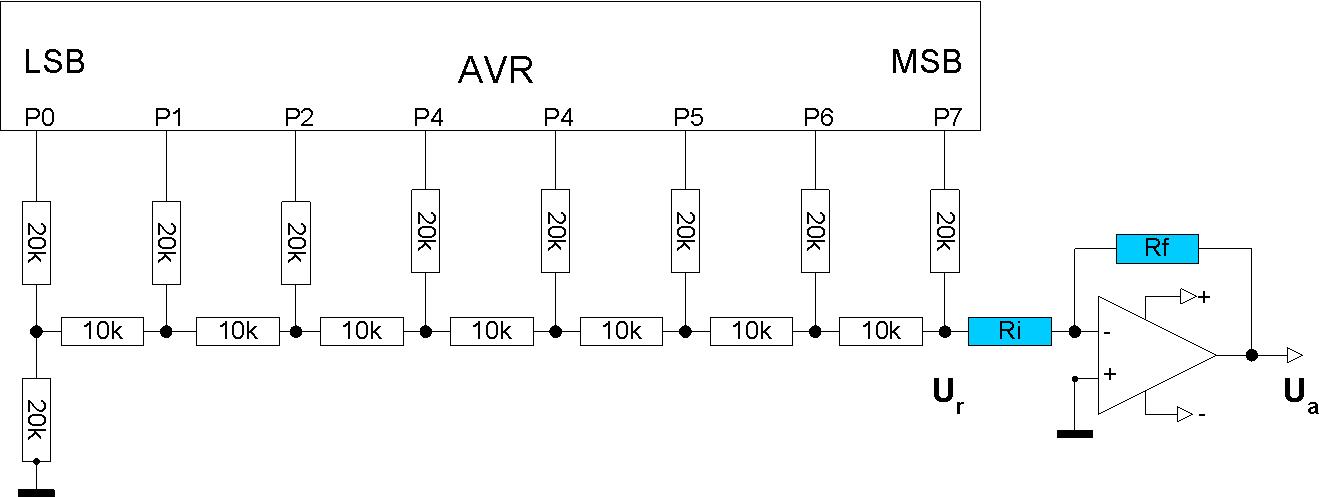
Abb. 1.1: R2R-Anordnung an einem AVR-Port.
Jeder Port-Pin kann die Zustände High (1=5V) oder Low (0=0V=Masse) einnehmen. Der OpAmp entkoppelt den DAC von der Folgeelektronik. Die Widerstandswerte 10k (R) und 20k (2R) sind offenbar Standard, wenn auch kein unumstößliches Diktat. Sie sollten einerseits eng toleriert sein (1% oder besser), andererseits hinreichend groß im Vergleich zum Innenwiderstand der AVR-Ports sein.
Des Rätsels Lösung zum Verständnis dieses Widerstandsnetzwerk-Puzzles ist das Thevenin-Theorem [7]: Wenn eine Schaltung aus linearen Elementen wie Spannungsquellen, Stromquellen und Widerständen besteht, kann sie an jedem Punkt aufgetrennt werden. Alles auf einer Seite des Schnittpunkts (nachfolgend links) kann durch eine Spannungsquelle und einem einzigen Widerstand in Serie ersetzt werden. Die Spannungsquelle ist die Leerlaufspannung am Schnittpunkt. Der Serienwiderstand ergibt sich, wenn alle Spannungsquellen nach Masse kurzgeschlossen werden.
Damit es nicht zu kompliziert wird, beschränken wir uns auf 4 Bits (P0 bis P3), an die die Bitfolge
(P3, P2, P1, P0) = 0001 gelegt wird. Die Spannung für logisch 1 ist Vr, am AVR +5V.
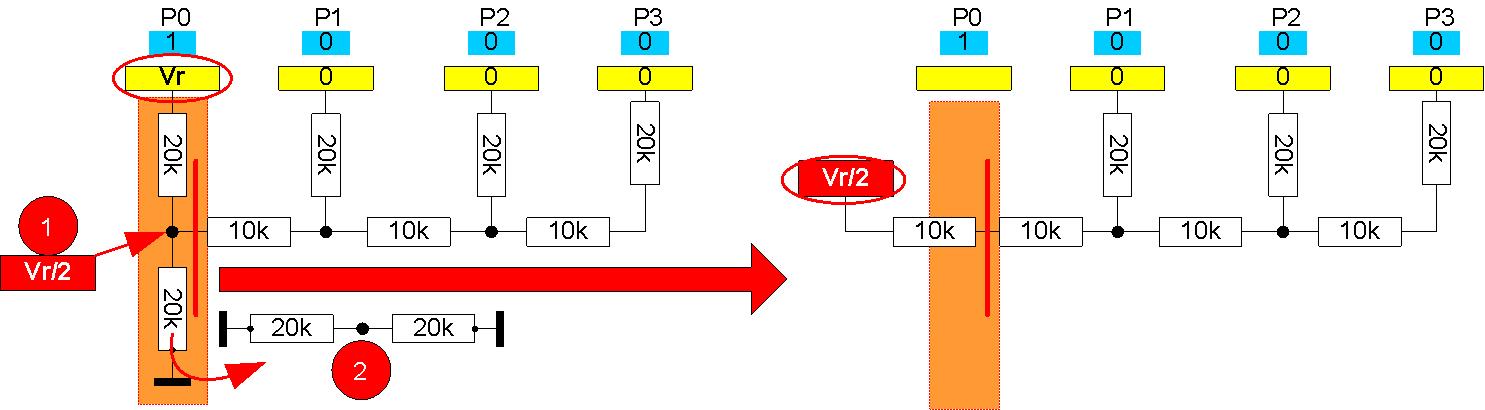
Abb. 1.2: Erste Zerlegung an P0.
- Die Leerlaufspannung zwischen den beiden 20k-Widerständen ist Vr/2.
- Wenn P0 nach Masse kurzgeschlossen wird, ergeben 2 Mal 20k parallel = 10k. Damit ist der wirksame Serienwiderstand an Vr/2 nun 2 Mal 10K = 20k (rechte Seite in Abb. 1.2).
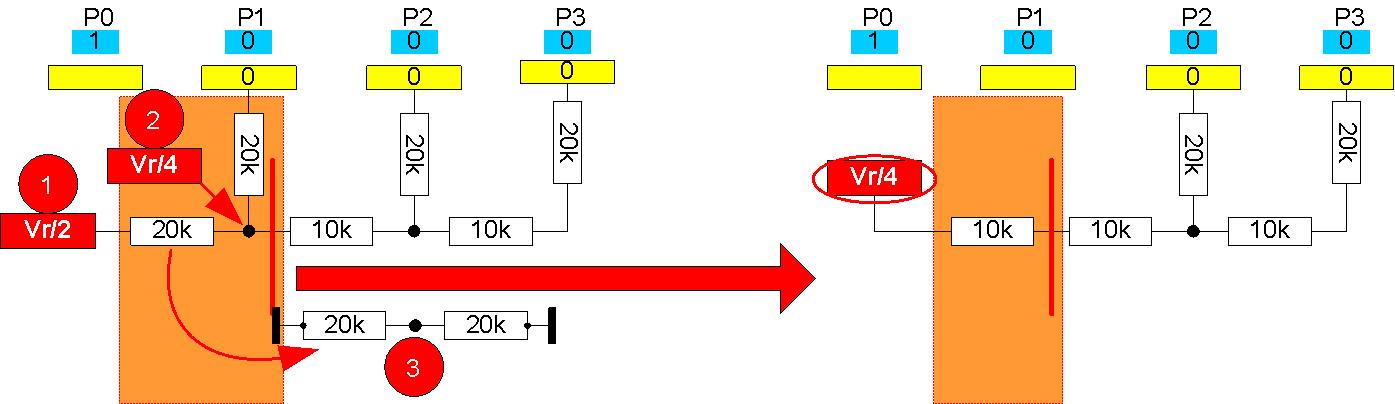
Abb. 1.3: Zweite Zerlegung an P1.
- Speisespannung ist nun Vr/2
- Die Leerlaufspannung zwischen den beiden 20k-Widerständen ist Vr/4.
- Wenn beide Spannungsquellen (P1 und Vr/2) nach Masse kurzgeschlossen werden, ergeben 2 Mal 20k parallel = 10k. Damit ist der wirksame Serienwiderstand an Vr/4 nun 2 Mal 10K = 20k (rechte Seite in Abb. 1.3).
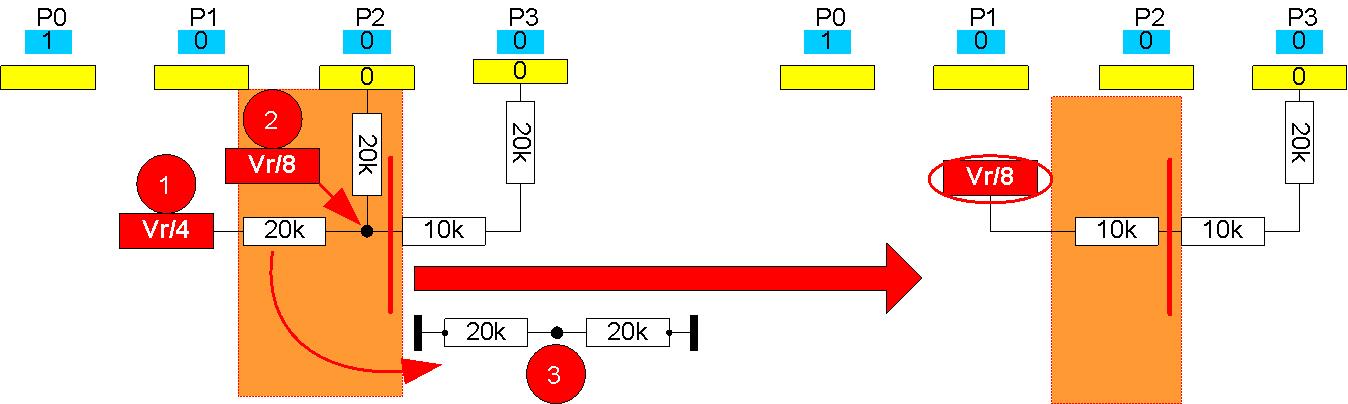
Abb. 1.4: Dritte Zerlegung an P2.
- Speisespannung ist nun Vr/4.
- Die Leerlaufspannung zwischen den beiden 20k-Widerständen ist Vr/8.
- Wenn beide Spannungsquellen (P2 und Vr/4) nach Masse kurzgeschlossen werden, ergeben 2 Mal 20k parallel = 10k. Damit ist der wirksame Serienwiderstand an Vr/8 nun 2 Mal 10K = 20k (rechte Seite in Abb. 1.4).
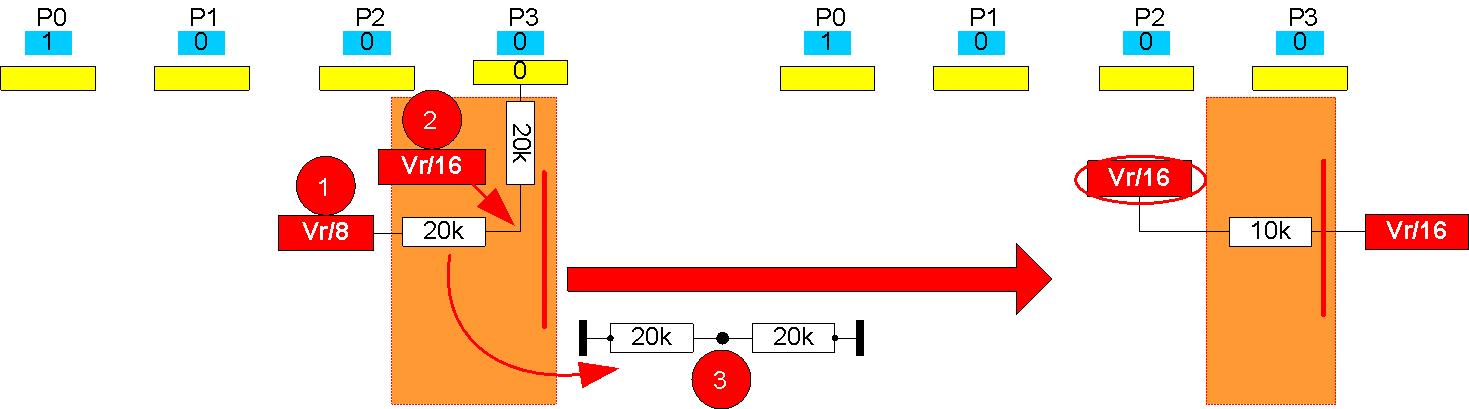
Abb. 1.5: Vierte und letzte Zerlegung an P3.
- Speisespannung ist nun Vr/8.
- Die Leerlaufspannung zwischen den beiden 20k-Widerständen ist Vr/16.
- Wenn beide Spannungsquellen (P3 und Vr/8) nach Masse kurzgeschlossen werden, ergeben 2 Mal 20k parallel = 10k als Ausgangswiderstand (rechte Seite in Abb. 1.5).
Ergebnis: Für die Bitfolge 0001 (=dezimal 1) erzeugt die R2R-Widerstandskette am unbelasteten Ausgang eine Spannung Vr / 16 (16 = 2^4) bei 4 Bit Auflösung.
Wenn dieses Simpelbeispiel mit variablen Bitfolgen an P0 bis P3 erweitert wird, ergibt sich am Ausgang der R2R-Kette:
Ur = Vr { P0 / 16 + P1 / 8 + P2 / 4 + P3 / 2 } mit P0...P3 = 0 oder 1.
Für die Bitfolge 0000 ist Ur = 0.
Für die Bitfolge 1111 ist Ur = Vr {1/16 + 1/8 + 1/4 + 1/2) = 0,9375 * Vr.
Munter erweitert auf die 8 Bit-Konfiguration nach Abb. 1.1 (2^8=256):
Ur = Vr { P0 / 256 + P1 / 128 + P2 / 64 + P3 / 32 + P4 / 16 + P5 / 8 + P6 / 4 + P7 / 2 }.
Für die Bitfolge 00000000 ist Ur = 0.
Für die Bitfolge 11111111 ist Ur = Vr {1/256 + 1/128 + ... + 1/2) = 0,9961 * Vr.
Der invertierende OpAmp (Abb. 1.1) verstärkt diese Spannung um den Faktor -(Rf / Ri).
Mit Vr = 5V ergibt sich also als kleinste Stufung 5/256 = 19,5 mV bei der 8 Bit-Kette. Oder andersherum für die Zeitachse über eine zu erzeugende Schwingungsperiode: Die Schwingung, z.B. eine Sinusperiode, kann in max. 256 Zeitabschnitte zerlegt werden. Da es ein AVR nun doch nicht schafft, für jede Zeitscheibe den Sinus zu berechnen, werden gespeicherte Lookup-Tabellen (LUT) verwendet. In diesen sind die gerundeten Funktionswerte der gewünschten Schwingungsform abgelegt, hier, passend zur Zeitauflösung, mit 8 Bit (1 Byte) Genauigkeit. Da das Byte kein Vorzeichen +/- kann, sind die Funktionswerte so verschoben, dass der Minimalwert Null ist. Die Werte für einen Sinus (-1 bis +1) bewegen sich also von 0 [sin(270°)=-1] bis 255 [sin(90°)=+1]. Die Nulllinie für sin(0°) entspricht damit dem Wert 127. Einfach ist es beim Rechteck: eine Periodenhälfte ist 0, die zweite ist 255.
1.2 Software-DDS
Wie wird nun die Bitfolge für den DAC erzeugt? Das alles versteckt sich in der Software des AVR, die offenbar auf den Assembler-Code von Jesper Hansen [1] zurückgeht. Wie eine DDS funktioniert, haben schon kundigere Leute als ich beschrieben, z.B. [8], [9]. Hier in Kürze:
Ein DDS besteht aus drei Funktionsblöcken, die hier im AVR einschl. diskreter DAC-Widerstandskette nachgebildet sind.
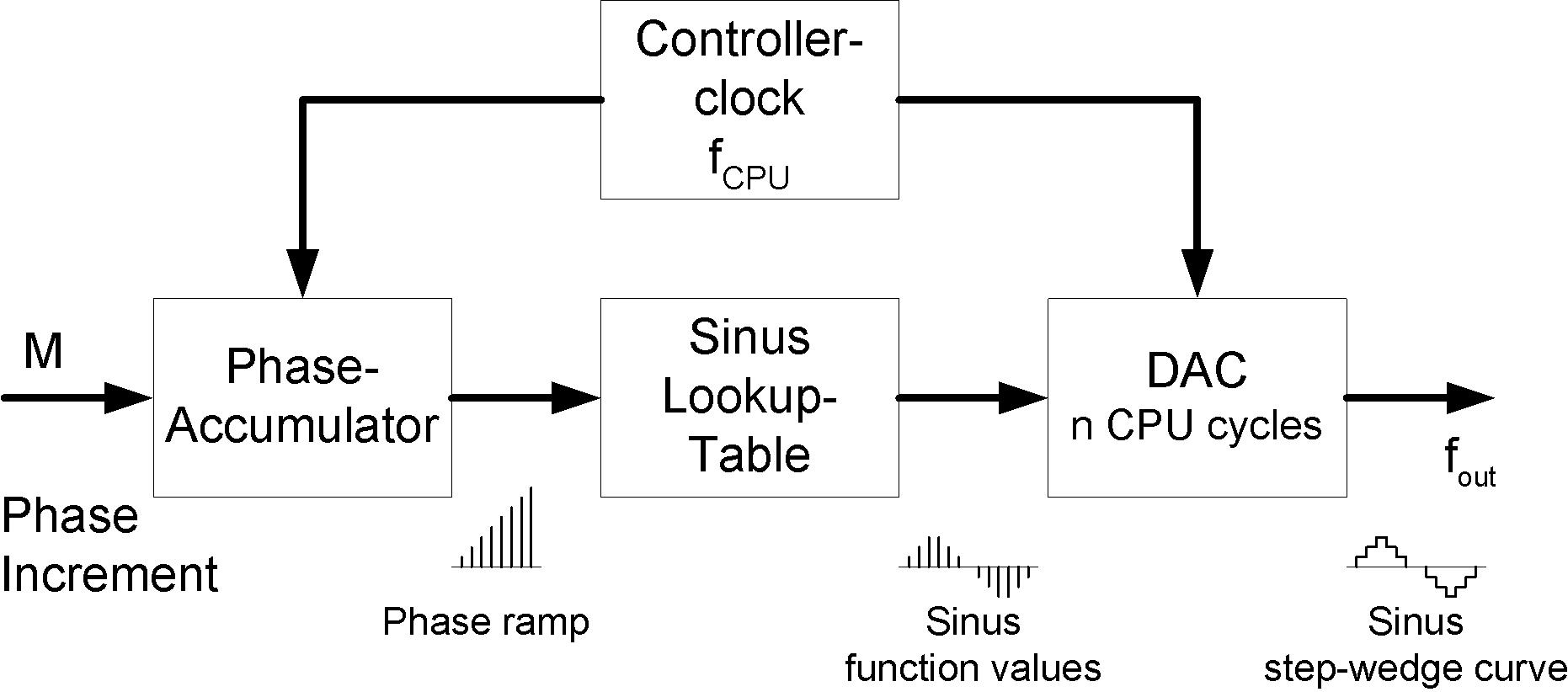
Abb. 1.6: Funktionsblöcke des DDS.
Im Phasenakkumulator werden die u.a. aus der gewünschten Ausgangsfrequenz fout bestimmten Phaseninkremente zu einer Phasenrampe aufsummiert.
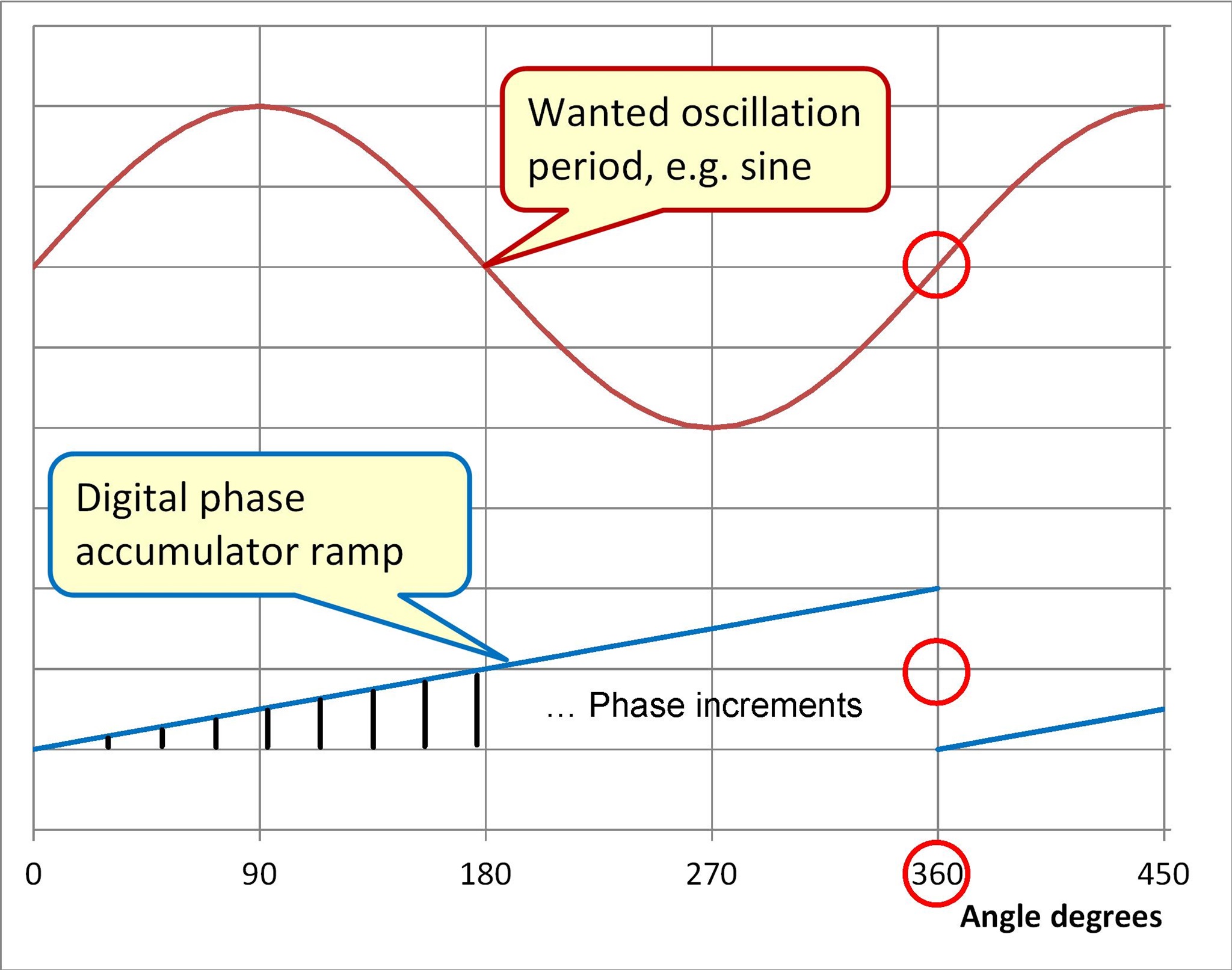
Abb. 1.7: Digitalisierung einer Schwingungsperiode, hier Sinus.
Die Phaseninkremente M ergeben sich aus
M = fout * Breite des Phasenakkumulators / Controller-Takt fCPU
Im AVR-Programm festgelegte Werte:
fCPU = 16 MHz
Breite des Phasenakkumulators: N = 24 Bit, also 2^N = 16.777.216.
Das Schreiben der Sinus-Funktionswerte aus der Lookup-Tabelle in den DAC benötigt ein paar CPU-Takte, im hier verwendeten AVR-Programm sind es n = 10. Um diesen Faktor reduziert sich der verfügbare CPU-Takt. Damit wird das Phaseninkrement für eine bestimmte Wunschfrequenz fout
M = fout * 2^N / (fCPU / n)
Der Kehrwert des Faktors 2^N... ist nichts anders als die aus dem CPU-Takt und der Phasenakkumulator-Breite resultierende Frequenzauflösung, im AVR-Programm "resolution":
Resolution = fCPU / (2^N * n)
Resolution = 16.000.000 / (16.777.216 * 10) = 0,0953674...
Den Charme an dieser in Software gegossenen DDS machen die Lookup-Tabellen aus, in Abb. 1.6 für einen Sinus dargestellt. Damit können beliebige Kurvenformen erzeugt werden, in dieser Anwendung auch Sägezahn, Dreieck und Rechteck, ja sogar EKG. Dafür gehen andere Leute zum Arzt.
| « Armeleute-DDS-Funktionsgenerator | TOP | » 2 Schaltung |