Quarze und Quarzfilter mit dem VNWA messen

Erstellt: DL6GL, 16.06.2021, letzte Änderung

Bei der Erkundung der Möglichkeiten meines kürzlich in Betrieb genommenen VNWA machte mich die Funktion "Crystal Analyzer" unter "Tools" neugierig. 2011 hatte ich mit dem FA-NWT Quarze vermessen, um damit verschiedene Quarzfilter für den TRX zu bauen [1]. Nicht, dass ich diese ersetzen wollte. Es interessierte mich, wie das mit dem VNWA zu machen ist. Im VNWA-Help sind dazu Hinweise dokumentiert; einige weitere Quellen unter Referenzen. Quarze aus meinen damaligen Versuchen waren genügend vorhanden. Als noch VNWA-Newbie habe ich einige Schritte mit dem VNWA ausführlicher beschrieben. Könner mögen mir das nachsehen. Ich übe noch.

1  Quarze messen

Zunächst ist eine Testvorrichtung nötig. Die wurde aus Buchsen- und Steckerleisten hergestellt. Als Load sind zwei SMA 0805 100Ω / 0,1% parallel verlötet.

Abb. 1.1: Test Fixture.

Das Resonanzverhalten eines Schwingquarzes lässt sich mit elektrischen Größen beschreiben.

Abb. 1.2: Ersatzschaltbild eines Schwingquarzes.

Die Induktivität Lm (m für "motional") charakterisiert die schwingende Masse,
die Kapazität Cm das Elastizitätsmodul des Quarzkristalls,
der Widerstand Rm mechanische Verluste im Kristallgitter,
die Kapazität C0 die Kapazität der beidseitigen Elektroden.

Ein Quarz hat zwei ausgeprägte Resonanzen, Serien- und Parallelresonanz. Uns interessiert hier die etwas tiefer liegende Serienresonanz. Sie lässt sich aus dem Impedanzverlauf, also einer S11-Reflexionsmessung, mit dem VNWA bestimmen. Eine Zweitormessung wäre auch möglich, erfordert aber eine aufwendigere Testvorrichtung.

1.1   VNWA einrichten

Die meisten Menüfunktionen sind auch mit Shortcuts aufzurufen, hier zur Verdeutlichung jedoch mit den Menübezeichnungen.

Zur Berechnung der o.a. Quarzparameter mit den VNWA Crystal Analyzer müssen Serien- und Parallelresonanz im gemessenen Frequenzbereich (Span) liegen. Oft (s.u. Referenzen) wird dieser mit 100kHz so groß bemessen, dass diese Bedingung sicher erfüllt ist. Das verlangt für eine akzeptable Auflösung eine hohe Anzahl Messpunkte (> 1.000) mit entsprechend geringer Messzeit pro Messpunkt. Einer Empfehlung von Kurt Poulsen, OZ7OU, folgend, habe ich mir angewöhnt, mit langer Messzeit pro Messpunkt und entsprechend geringerer Auflösung zu messen, nachfolgend bei der Ausmessung der Quarze mit 500 Punkten und 60ms je Punkt. Ein Vergleich 3.000/10ms zu 500/60ms aus je 6 Messungen an einem Quarz ergab allerdings keine signifikanten Abweichungen (Serien-Resonanzfrequenz < 1Hz, Q < 0,4%, Lm und Cm < 0,02%, C0 < 0,2%, Rm < 0,4%). Ich bin dennoch bei 500 Punkten geblieben, damit wird das Smith-Diagramm halt etwas eckig.

Damit die nur 500 Messpunkte eine akzeptable Frequenzauflösung gewährleisten, wurden ohne gesonderte Kalibrierung Durchgangsmessungen (S11 + S21) an einigen Quarzen durchgeführt, um einen angemessenen Frequenzbereich für Serien- und Parallelresonanz festzulegen.

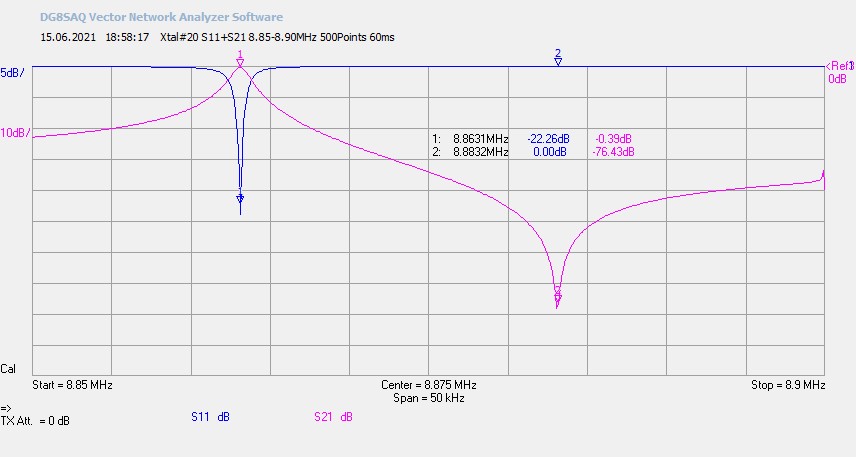
Abb. 1.3: Festgelegter Frequenzbereich 8,85 - 8,90MHz (Span 50kHz) für Serien- und Parallelresonanz.

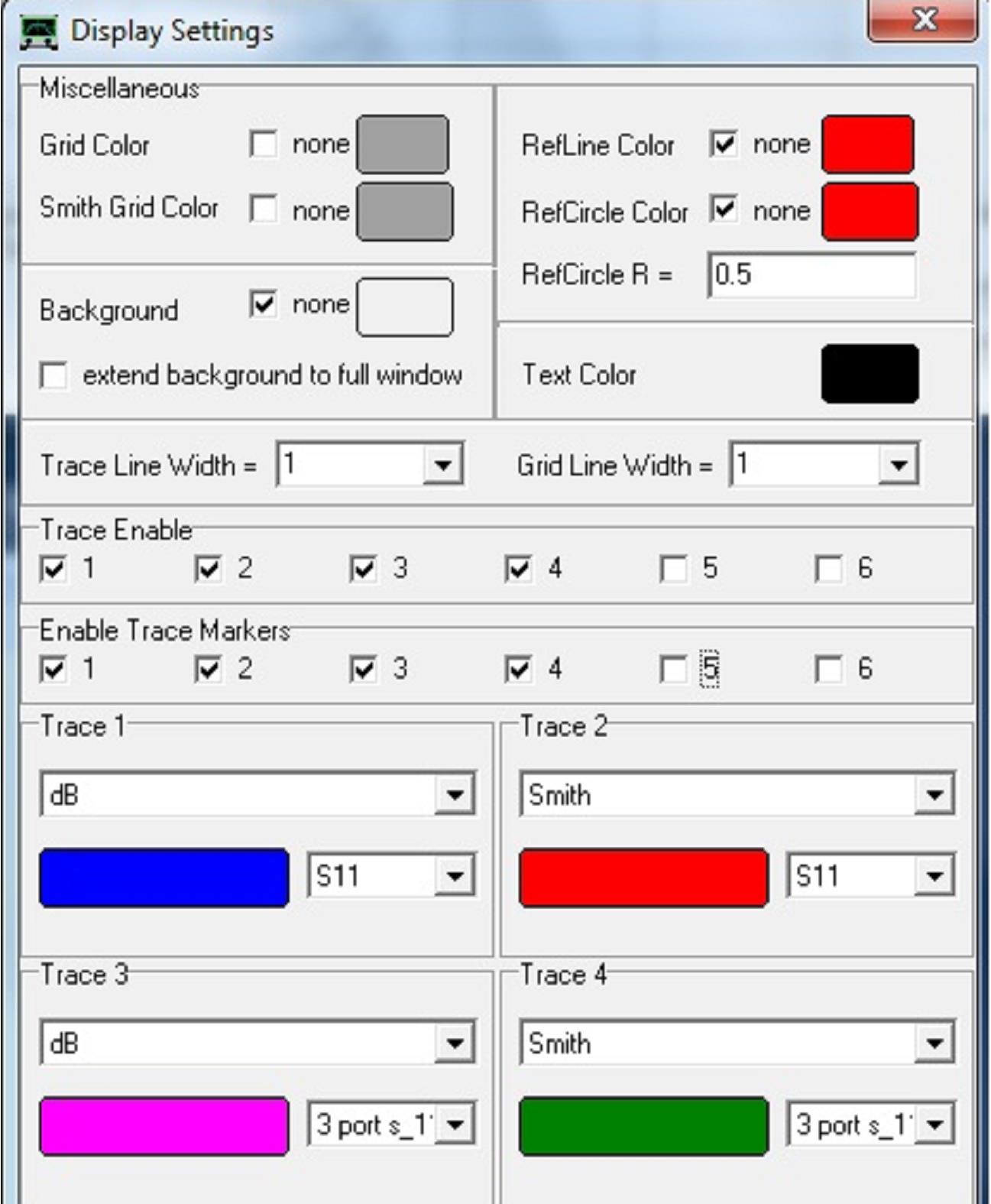
Abb. 1.4: Traces für die S11-Quarzmessung.

• Settings – Frequency Range, damit Frequenzbereich festlegen:
   für die hier zu messenden 8,8672MHz-Quarze: 8.85 bis 8.90MHz (Span 50kHz).
• Settings – Diagrams – Display – Traces: S11, s_11 (dB) und S11, s_11 (Smith).
  s_11 für die Berechnungen aus den Quarzparametern, in Traces als "3 port s_11" ausgewählt.
• Settings – Sweep: Hier z.B. 500 Data points, 60ms per Data point.
• Settings – Calibration Kit: SOLT ideal calibration standards.
  Von unseren SOL-Standards (Abb. 1.1) ist außer Load ~50Ω nichts bekannt, also "ideal…standards". Das ist gut genug für Quarze um die 10MHz.

Abb. 1.5: Calibration Settings: ideal calibration standards.

Mit diesen Settings kann nun eine Kalibrierung der Test Fixture vorgenommen werden.
Measure – Calibrate: Nur Short, Open und Load (SOL) mit den Steckersätzen in Abb. 1.1, anschließend mit "Exit" links oben die Kalibrierung beenden.

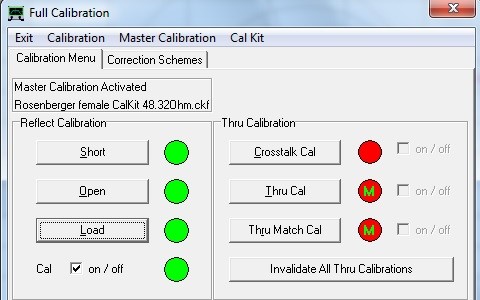
Abb. 1.6: SOL-Kalibrierung der Testvorrichtung.

1.2   Messungen

Da für die Auslegung des Quarzfilters mit dem Berechnungsprogramm weiter unten Quarze mit möglichst identischen Eigenschaften zu verwenden sind, muss eine ausreichende Menge zur Auswahl vorhanden sein. Die Quarzdaten streuen. Alle Quarze werden vorab nummeriert.

Unter "Tools – Crystal Analyzer" bietet der VNWA ein mächtiges Werkzeug, das aus der S11-Messung alle benötigten Quarz-Resonanzdaten extrahiert, vgl. Abb. 1.2.

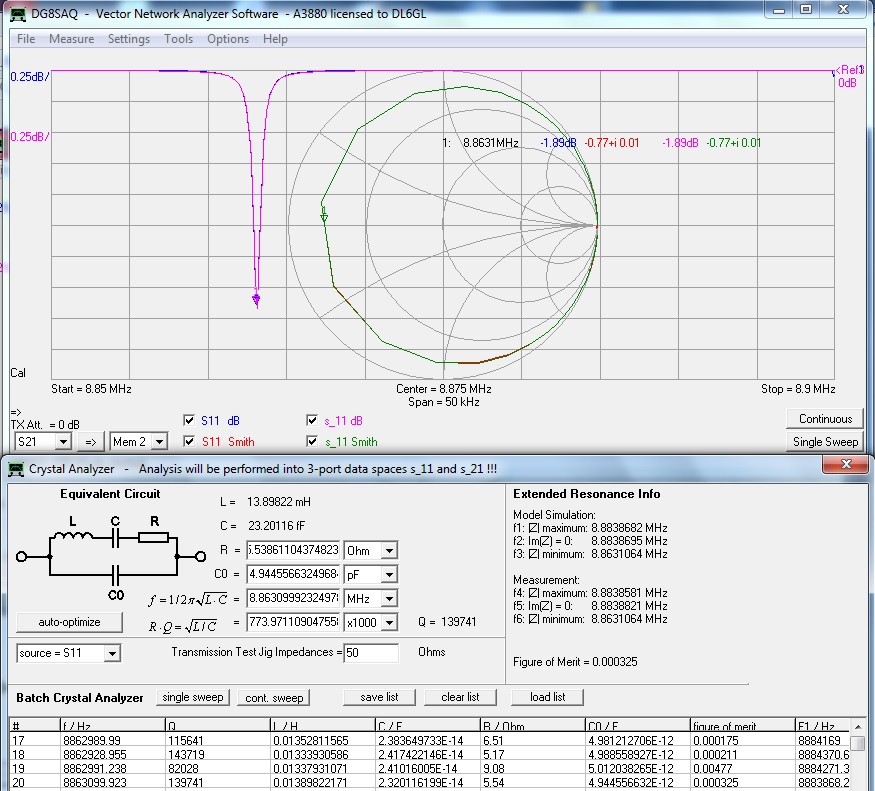
Abb. 1.7: VNWA Crystal Analyzer.

Erkennbar ist, dass die gemessene S11-Kurve (blau) und die aus den ermittelten elektrischen Quarzdaten berechnete s_11-Kurve (violett) deckungsgleich sind, ebenso die Smith-Diagramme. Die 500 Punkte-Auflösung bedingt die Polygonform an den relativ wenigen Stützstellen. 

Die Quarze werden nur mit einer Pinzette hantiert, um eine Erwärmung mit den Fingern zu vermeiden. Wenn eine längere Messreihe bevorsteht, sollten die Raumtemperatur konstant gehalten und in einem Zug gemessen werden.

• Start der Messung mit "Single Sweep"
• Nach einer Messung kann in der ersten Spalte die jeweilige Nummer überschrieben werden. Der VNWA inkrementiert die laufende Nummer automatisch.
• Wenn alle Quarze vermessen sind, kann die Liste mit "Save list" in ein .csv-File abgespeichert werden.
• Zur weiteren Verarbeitung, insbesondere Sortieren nach Resonanzfrequenz und Lm und gleichzeitig Güte Q > 100.000, steht ein Excel-Sheet "VNWA Xtal Measurements.xlsx" im Download zur Verfügung.
  Das aus dem Crystal Analyzer abgepeicherte .csv-File wird in die Tabelle "VNWA csv import" eingelesen.

Hier die zusammengefassten Ergebnisse.

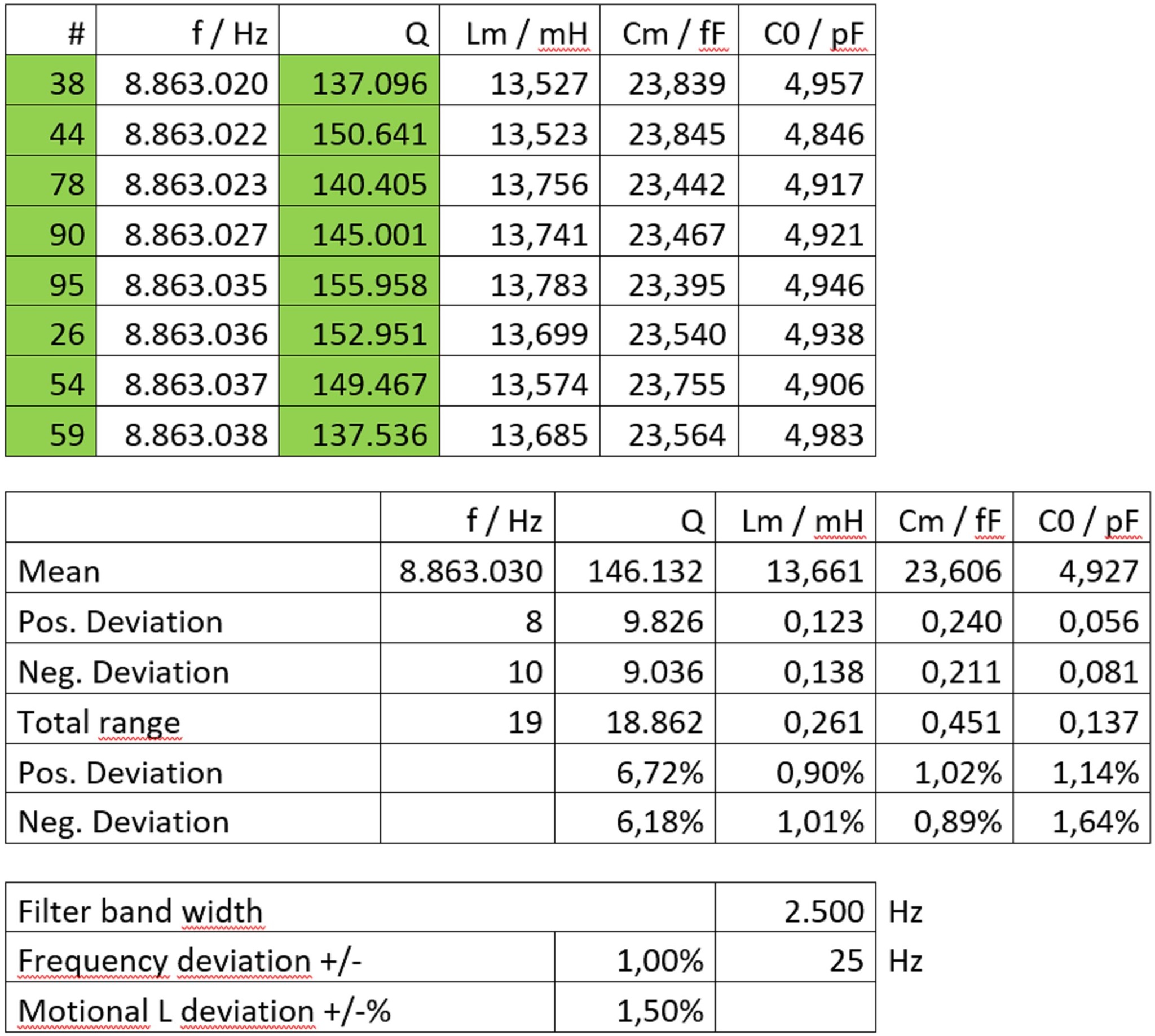
Tab. 1.1: Auswertung der Daten mit Excel.

Die Frequenzabweichung sollte max. +/- 1% der geplanten Filterbandbreite sein.
Lm sollte maximal um +/- 1,5% streuen. Das ist bei der obigen Auswahl gegeben.

2   Quarzfilter berechnen

Die Mittelwerte aus den Quarzdaten finden Eingang in ein Berechnungsprogramm für Quarzfilter, nachfolgend für Dishal 2.0.5.2 von DJ6EV. Es werden also alle Quarze als identisch angenommen. Deshalb sollten die Streuungen um die Mittelwerte (Serien-Resonanzfrequenz, Lm, wahlweise Cm, und C0/Cp) möglichst gering sein. Dishal 2.0.5.2 ist in [3] zu finden.

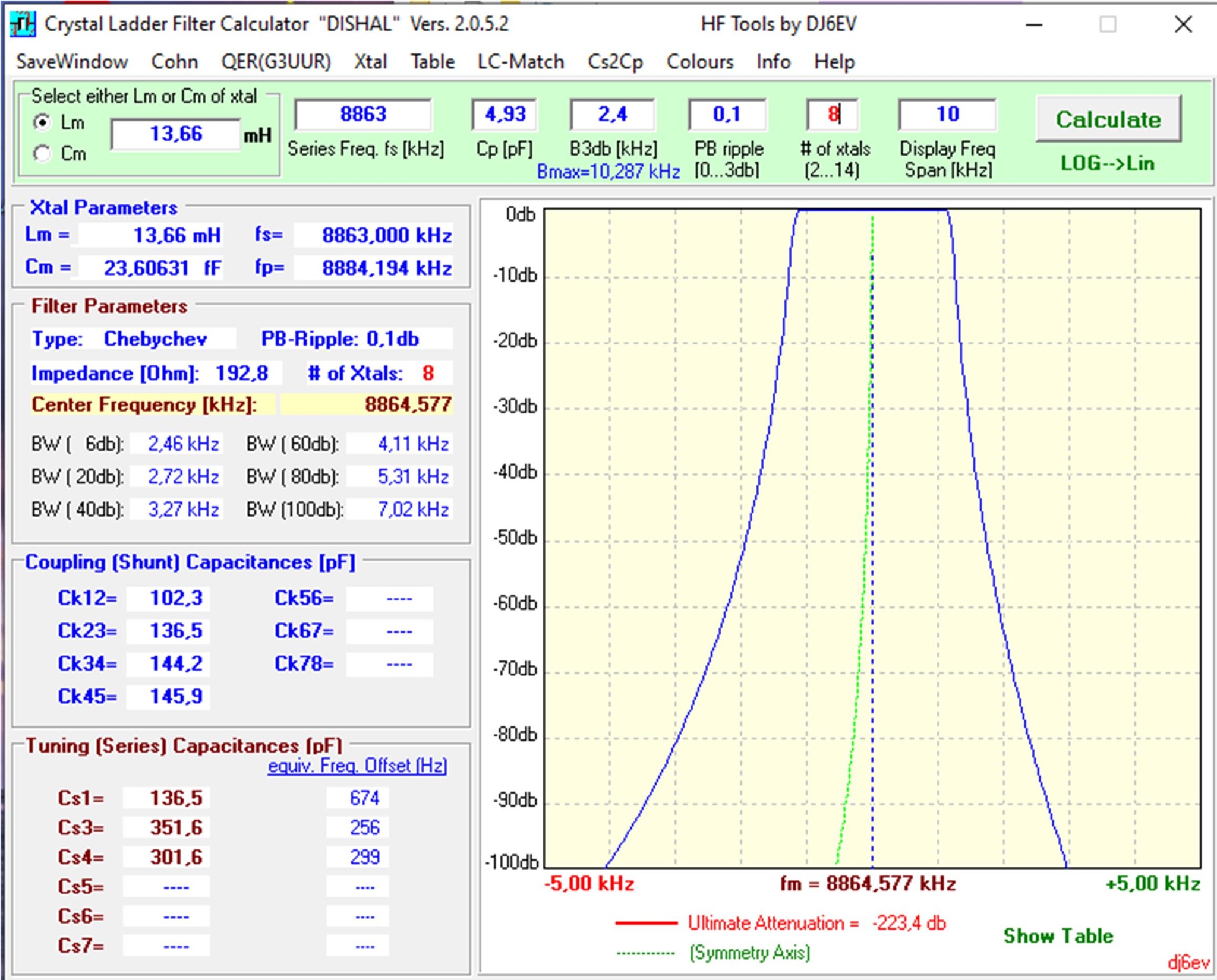
Abb. 2.1: Filterberechnung mit Dishal 2.0.5.2.

Abb. 2.2: Nummerierung der C's für ein 8-Pol-Quarzfilter.

Die ermittelten Kondensatorwerte geben uns nun Anhaltspunkte, in Tüten und Schachteln nach passenden Werten zu suchen, die, zumeist in Kombination zweier C's, den Sollwerten annähernd gleichkommen. COG/NP0-Typen wären die besten Aspiranten. Ausgemessen wurden sie mit dem AADE L/C Meter IIB. Der VNWA könnte das auch mit der Testvorrichtung in Abb.1.1, siehe z.B. [6].

Abb. 2.3: Filteraufbau im Dead-Bug-Style auf einem Platinenabschnitt.

Die Quarze werden mit Wäscheklammern auf die Kupferfläche aufgeklemmt. Auch wenn das wüst aussieht, war bei den auf diese Weise in 2011 vorab getesteten Filtern keine signifikante Abweichung zum endgültigen Aufbau mit einer geätzten Leiterplatte und SMD-C's festzustellen. Layouts der damals realisierten Filter sind in [1] zu finden.

3   Messung des Quarzfilters

Die vormalige SOL-Kalibrierung ist natürlich untauglich für die Messung am fertigen Filter. Es steht also eine neue SOLT-Kalibrierung an. Die Settings sind hierfür zu ändern.

• Settings – Frequency Range, reduziert auf 8.855 - 8.875MHz, Span 20kHz.
• Settings – Diagrams – Display – Traces: S11 (dB), S11 (Smith), S21 (dB), S22 (dB) und S12 (dB).
  S22 und S12 werden für das Matching gebraucht.
• Settings – Sweep: Hier z.B. 300 Data points, 100ms per Data point.
• Settings – Calibration Kit: SOLT simple model custom calibration standards
  mit Daten des vorhandenen Cal Kit, hier Rosenberger female Cal Kit.

Abb. 3.1: Auswahl der Traces für 12 Term correction.

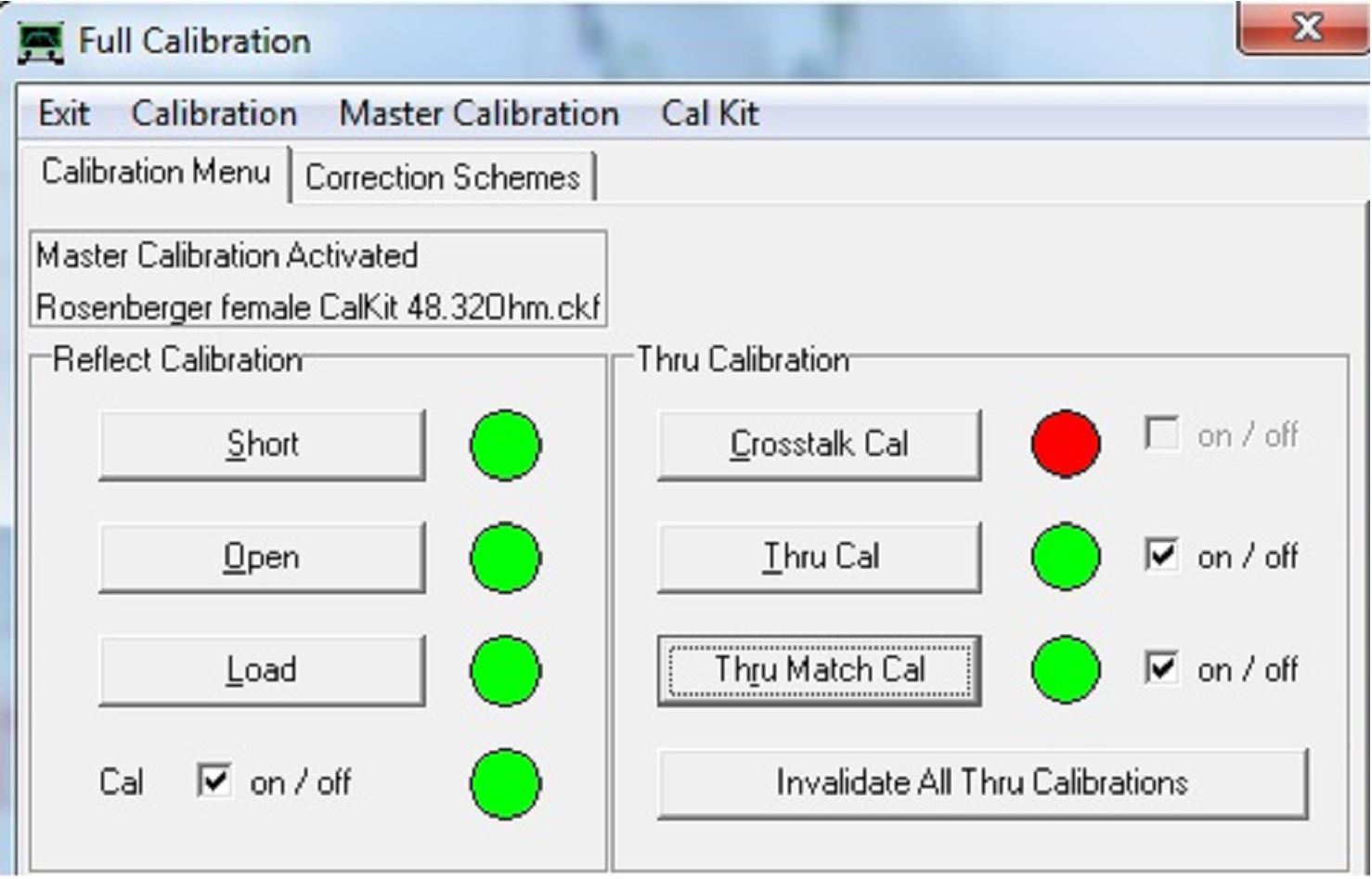
Abb. 3.2: SOLT-Kalibrierung 8.855 – 8.875MHz für das Quarzfilter.

Dishal lieferte eine Filterimpedanz von 192,8Ω. Die Quarzverluste Rm berücksichtigt Dishal dabei nicht. Rechnungen sind eine Sache. Mal sehen, was der VNWA mit seinem Matching Tool unter "Options" aus den Messungen dazu sagt. Das Matching Tool braucht alle vier S-Parameter (12 Term Correction). Ohne das S-Parameter Test-Set geht das zu Fuß in zwei Messungen mit der F2-Taste. Für die zweite Messung werden TX und RX vertauscht (Vor- und Rückwärtsmessung). Das Filter wird ohne Anpassung (Matching, Abb. 2.2) gemessen. Die Ringkerne in Abb. 2.3 sind also entfernt.

Abb. 3.3: Matching tool, Optimierung der Durchlasskurve mit Port Impedance.

Der Durchlassbereich ist mit der Vorbesetzung Port 1 Impedance = Port 2 Impedance = 50Ω wellig. Um dem abzuhelfen, werden die Ein- und Ausgangsimpedanz wie in Abb. 3.3 geändert. Die Auswirkung einer Änderung (Cursor in das Feld für die Port 1 Impedance, Änderung mit dem Mausrad) ist im Plot sofort erkennbar - einfach begeisternd. Bei 225Ω war ein Optimum bzgl. Durchlassbereich und Return Loss (S11) erreicht. Die Eingangskapazitäten "C parallel" haben nur einen geringen Einfluss. Sie wurden mit C  = 0 belassen. Mit etwas gutem Willen sind sich also Dishal und VNWA halbwegs einig.

Weiter zu erkennen ist, dass S11 (blau) und S22 (grün) sowie S21 (rot) und S12 (orange) nahezu identisch sind, auch wenn die Durchlasskurven (S11, S21, vorwärts) und (S22, S12, rückwärts) für die gewählte Anpassung berechnet sind. Trotz der unvermeidbaren Toleranzen der zumeist zusammengesetzten C's ist das Filter somit in guter Näherung spiegelsymmetrisch.

Erstaunlich ist die große Sperrdämpfung trotz des fliegenden Aufbaus (Abb. 2.3).

Die Matching Network Variant Nr. 2 bietet ein alternatives LC-Filter mit L seriell und C als Shunt an.

Die Marker wurden manuell positioniert.

Nun gilt es, das vom VNWA vorgeschlagene Matching auf 50Ω als LC-Filter einzufügen. Die 2,15 μH Induktivität wurde mit 17 Windungen 0,22mm CuL auf T25-2 gewickelt.

Wegen der o.g. guten Spiegelsymmetrie wurden nachfolgende Plots nur in einer Richtung aufgenommen.

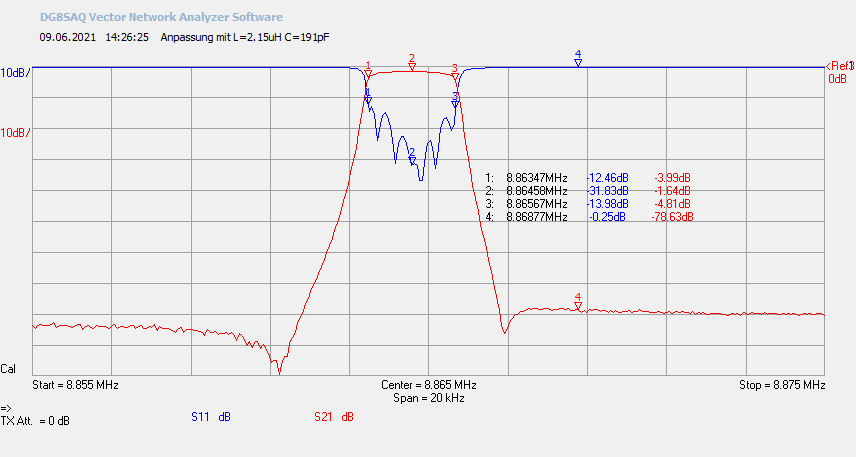
Abb. 3.4: Anpassung mit L=2,15μH (Shunt), C=191pF(seriell).

Der Durchlassbereich ist annähernd identisch mit der Berechnung des Matching-Tools. Aber der Sperrbereich ist von ~ -90dB bis auf ~ -78dB im oberen Segment angestiegen.

Das Impedanzverhältnis 50:~200Ω legt die Verwendung eines Bifilar-Autotrafos mit Z-Transformation 1:4 statt der LC-Glieder (Abb. 3.4) nahe.

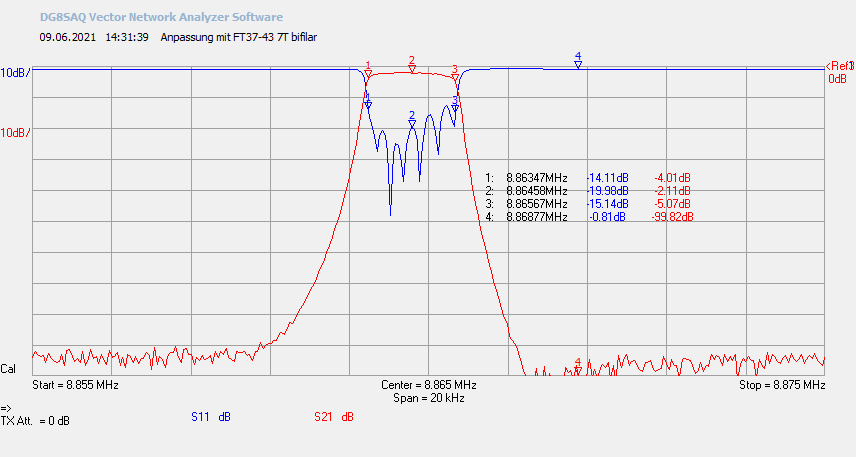
Abb. 3.5: Anpassung mit FT37-43, 2x7 Windungen bifilar.

Das Ergebnis ist besser als mit dem LC-Matching. Insbesondere wird der Sperrbereich stärker gedämpft (-78,6 zu ~ 90dB).

Der Vollständigkeit halber wurde noch ein Z = 1:4-Transformator mit BN43-2402, 2+4 Windungen, versucht. Wie im symmetrisch bifilar gewickelten Ringkern-Autotrafo mit Windungsverhältnis 1:2 erlauben Transformatoren mit ganzzahligen Windungsverhältnissen nur eine angenäherte Anpassung, die hier ausreichend erscheint. Anmerkungen hierzu:

1. Wenn der Autotrafo asymmetrisch, also mit ungleichen Primär- und Sekundärwicklungen angelegt wird, sind auch höhere Impedanzverhältnisse als 1:4 herzustellen.
   
2. Es ist bei allen Transformatoranpassungen darauf zu achten, dass die Wicklungsimpedanzen Z=2*π*f*L mindestens 10*Anschlussimpedanz sind. Bei den 2 Windungen auf BN43-2402 (Z~340Ω bei 8,86MHz für eine Anpassung an 50Ω) ist das schon grenzwertig. Hier wären 3:6 Windungen passender gewesen.
3. Wegen der geringeren Streufeldverluste sind Doppellochkerne wie der BN43-2402 geeigneter als Ringkerne, Verschaltung als Autotrafo etwas besser als isolierte Wicklungen.

Abb. 3.6: Anpassung mit BN43-2402 2+4 Windungen (Transformation 50:200Ω).

Die Durchlassdämpfung ist etwas höher als mit dem 1:4-Autotrafo. Der Sperrbereich ist akzeptabel.

Zur Vervollständigung noch die gemessenen Bandbreiten für die Variante mit Autotrafo-Anpassung (Abb. 3.5).

Abb. 3.7: 3dB-Bandbreite, gemessen mit 12 Term Correction.

Die Bandbreitenmarker erhält man nach Rechtsklick auf den Plot, Add Frequency Marker - Bandwidth - Bandpass.

Die rechts in dem vierzeiligen Textfeld in Zeile 2 angezeigte Standardbandbreite 10dB lässt sich mit Rechtsklick in das Textfeld anpassen: Set bandwidth level.

Die 3dB-Bandbreite von 2,23kHz ist deutlich kleiner als mit Dishal berechnet (2,4kHz).
Mit den Bandbreiten 6dB (2,36kHz) und 60dB (4,11kHz) ergibt sich ein Formfaktor 1,74, Durchlassdämpfung 2dB.

4   Bewertung

So war es damals in 2011 mit dem FA-NWT [1]:

• Der skalare FA-NWT ist intuitiv zu bedienen. Die Kalibrierung ist mit zwei Messungen ein Kinderspiel.
• Ein Test Fixture 50Ω →12,5Ω → 50Ω ist zu bauen. Die resultierende Gesamtabschwächung von ca. 30dB erfordert einen Aufholverstärker.
• Zur Ermittlung der statischen Parallelkapazität der Quarze ist ein Messgerät erforderlich.
• Die Serien-Resonanzfrequenz und die 3dB-Bandbreite liefert der NWT. Die Daten müssen abgelesen und in ein Excel-Sheet übertragen werden.
• Im Excel-Sheet müssen verschiedene Formeln programmiert werden, um die Parameter der Quarz-Ersatzschaltung zu bestimmen.
• Die Entwicklung des FA-NWT 1 ist seit langem eingestellt. Es gibt aber einen Nachfolger.

So zeigte es sich nun mit dem DG8SAQ-VNWA:

• Der Umgang mit dem VNWA ist nicht trivial. Es ist eine gründliche Einarbeitung über das Help-File und mit Sekundärliteratur unerlässlich. Die Kalibrierung ist aufwendiger, aber eigentlich simpel, muss aber in der Regel für geänderte Messkonfigurationen neu durchgeführt werden; Ausweg: Master Calibration.
• Ein einfaches Test Fixture ist schnell erstellt. Weitere Hardware ist nicht erforderlich.
• Wenn Bedienung und Menüstruktur erst einmal durchschaut sind, kommen darin mächtige Funktionen zum Vorschein, die alle weiteren Bestimmungen der Quarz- und Filterparameter zu einem Erlebnis machen. Das Matching-Tool ist der absolute Knüller.
• Der DG8SAQ-VNWA ist bis heute ein lebendes System dank fortlaufender Updates und Hilfestellungen von vielen Seiten im Netz und von Nutzern, selbst von Thomas Baier, DG8SAQ, "himself".

Referenzen

[1] dl6gl.de/selbstbau-trx/...quarzfilter
[2] https://www.bartelsos.de/filter/quarzfilter/quarzfilter
[3] https://www.bartelsos.de/filter/quarzfilter/quarzfilter-dj6ev
[4] https://www.bartelsos.de/_media/messtechnik/vnwa/workshop_notes_volume_2_deutsch.pdf
[5] https://www.darc.de/fileadmin/_migrated/content_uploads/Quarze_rev_1.4_df1rn_2014_10_11.pdf
[6] http://www.sdr-kits.net/DG8SAQ/VNWA/VNWA_Experiments.pdf

Download

VNWA Xtal_Measurements.xlsx