Impedanzanpassung - Matching

Erstellt: DL6GL, 25.09.2022, letzte Änderung 20.04.2024

Matching Anpassungsnetzwerk

Mit Impedanzanpassung schlägt sich jeder von uns Funkamateuren mal rum, sei es bei der Anpassung einer Antenne, um im RX noch die kleinsten Signale aufnehmen zu können oder die TX-Leistung möglichst verlustfrei in die Luft zu bringen. Oder einen Mischer oder ein Filter optimal zu betreiben. Bei Fehlanpassungen entstehen, oft Hauptursache von Leistungsverlusten, immer Reflexionen zurück in die Quelle, die dort Störungen hervorrufen. Oder bei Filtern werden die Durchlasskurven verbogen, wenn sie nicht auf die Auslegungsimpedanzen arbeiten.

Im Web gibt es an Onlinerechnern und Programmen alles, was Amateurherzen höherschlagen lässt. Nur wiederfinden im Netz oder im eigenen Computer muss man solche Goodies, wenn es gerade mal wieder pressiert. In der Vergangenheit habe ich bisweilen einige Auslegungshilfen erstellt, weil das ständige Suchen lästig wurde, natürlich mit MS Excel. Idee war, alle Fundstücke mal in einem Excel-Workbook (im Download) zusammenzustellen.

Es enthält Berechnungsblätter für:

L-Netzwerk zur Anpassung reeller Quell- und Lastimpedanzen,
L-Netzwerk zur Anpassung komplexer Quell- und Lastimpedanzen,
Anpassung mit Breitbandtransformatoren,
Pi- und T-Abschwächer, auch für Zin ≠ Zout,
Anpassung mit Resonanzkreisen (Simpelmodell, angezapfte C's und L's),
Anpassung mit Resonanzkreisen (Genaues Modell nach KJ6PO, angezapfte C's),
Neu (07.10.2022): Bridged Tee Diplexer für impedanzrichtigen Abschluss von Mischern.

Daten gängiger Amidon-Kerne sind über Kombinationsfelder zur konkreten Auslegung abrufbar.

Auf dieser Seite soll nur ein kurzer Blick auf das doch recht ergiebige Thema der Impedanzanpassung geworfen werden. Eine ausführlichere Erläuterung ist im Download ("Impedanzanpassung - Matching.pdf") zu finden. Insbesondere werden dort die Berechnungsgrundlagen für das häufig verwendete L-Netzwerk (1), den "Tapped Capacitor"-Resonanzkreis (6) und den Bridged Tee Diplexer (7) näher betrachtet.

1 Worum geht es bei einer Anpassung?

Es ist die maximal mögliche Leistung von einem Modul (Quelle) auf ein anderes (Last) zu übertragen, auch wenn sich die jeweiligen Impedanzen unterscheiden. Wenn möglich ohne Leistungsverlust. Dann sind Quelle und Last einander angepasst.

Im einfachsten Fall, einem Gleichstromkreis, sieht das etwa so aus:

Power transfer

Abb. 1.1: Leistungsübertragung mit einem Gleichspannungsteiler.

Was wir schon immer ahnten:
Die maximale Leistungsübertragung erfolgt bei Anpassung
Quellimpedanz = Lastimpedanz.

Das Beispiel in Abb. 1.1 mit ohmschen Widerständen ist ja ganz nett, die Anpassungsbedingung RS = RL zu demonstrieren, viel haben wir mit solch einem Spannungsteiler aber anscheinend nicht gekonnt. Die Spannung wird bei Leistungsanpassung auf die Hälfte geteilt, die Leistung über U^2/R auf ein Viertel. Die wird zumindest für RS=RL maximal übertragen. Mehr geht hier nicht.

Das ist aber genau der Ansatz der uns geläufigen 50Ω-Technik. Um HF-Module/-Geräte mit reell 50Ω Eingangs- und Ausgangsimpedanzen zu verbinden, geht es um maximale Leistungsübertragung mit minimalen Reflexionen. Mit anderen Worten: Die verfügbare Leistung wird in der Last vollständig aufgenommen und steht ohne Reflexionsverluste der weiteren Verarbeitung, z.B. einer Messung, zur Verfügung.

Wenn wir das auf Wechselstrom, also auf Hochfrequenz mit zumeist komplexen Impedanzen, ausdehnen, erfolgt die maximale Leistungsübertragung bei Anpassung für eine vorgegebene Frequenz bei
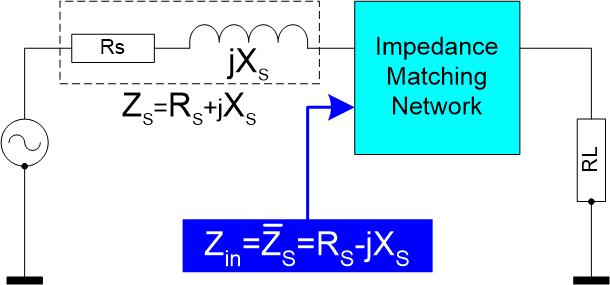
Lastimpedanz (Z_L= R_L+jX_L= ! R_S-jX_S) = komplex konjugierte Quellimpedanz (Z_S= R_S+jX_S).

Simple lC matching

Abb. 1.2: Beispiel für eine Anpassung mit konjugiert komplexen Impedanzen.

Für optimale Anpassung, hier mit RS = RL wie oben als einfachstes Beispiel, müssen sich die negative Reaktanz des Kondensators in ZL (-jXL) und die positive Reaktanz der Spule in ZS (jXS) aufheben.
Mit XS = 2πfL und XL = 1 / 2πfC ist die Anpassung nur für genau eine Frequenz f gegeben. Die Verschaltung von XS und XL entspricht einem Serienschwingkreis mit Resonanz bei Frequenz f. Mit Durchlasswiderstand Null bei Resonanz, also XS=-XL, haben wir also wieder den Zustand wie in Abb. 1.1. Zumindest im Idealfall mit verlustlosen L und C.

Allgemein gesprochen muss für eine Impedanzanpassung mit maximaler Leistungsübertragung die Lastimpedanz so erscheinen wie die konjugiert komplexe Quellimpedanz.

Impedance matching network

Abb. 1.3: Impedanzanpassung für komplexe Quelle und Last mit einem Anpassungsnetzwerk.

Das Anpassungsnetzwerk lässt die Lastimpedanz von der Quelle aus betrachtet so aussehen wie die konjugiert komplexe Quellimpedanz Zin=RS-jXS (negatives XS). Es gaukelt also der Quelle eine andere Impedanz vor, als tatsächlich in Form von ZL hinter dem Netzwerk anliegt.

Wenn im Anpassungsnetzwerk Blind-/Scheinwiderstände eingesetzt werden, also Reaktanzen in Form von als verlustlos angenommenen Induktivitäten und Kapazitäten, erfolgt bei Anpassung damit eine verlustlose Leistungsübertragung.

2 Anpassung mit L-Netzwerken

Ein beliebtes Anpassungsnetzwerk ist das in Form eines L, z.B. zur Anpassung komplexer Antennenimpedanzen an die reelle 50Ω-Impedanz eines TRX.

Lowpass, Highpass matching

Abb. 2.1: Die vier L-Netzwerke als Hoch- und Tiefpässe.

Je nach Verschaltung, das ist tatsächlich nur eine Spiegelung, erlauben sie eine Transformation
aufwärts (ZSoure < ZLoad) oder abwärts (ZSource > ZLoad)

Das serielle Element (L oder C) liegt an der niedrigeren Impedanz (Source oder Load).
Das parallele Element liegt an der höheren Impedanz (Source oder Load).

Neben der Funktion als Impedanz-Anpassungsnetzwerk unterscheiden sich beide Ausführungsformen

Filterfunktion, Tiefpass mit Dämpfung hoher Frequenzen und Hochpass mit Dämpfung niedriger Frequenzen,
Durchleitung von DC-Strömen, z.B. von/zu Transistorstufen, beim Tiefpass, Sperrung beim Hochpass.

Für den einfachen Fall - Zsource und ZLoad beide reell - ist die Herleitung der Berechnungsformeln für das Excel-Sheet in der Beschreibung im Download wiedergegeben. Für die Erweiterung auf komplexe Impedanzen, z.B. eine Antennenanpassung sieht das z.B. so aus:

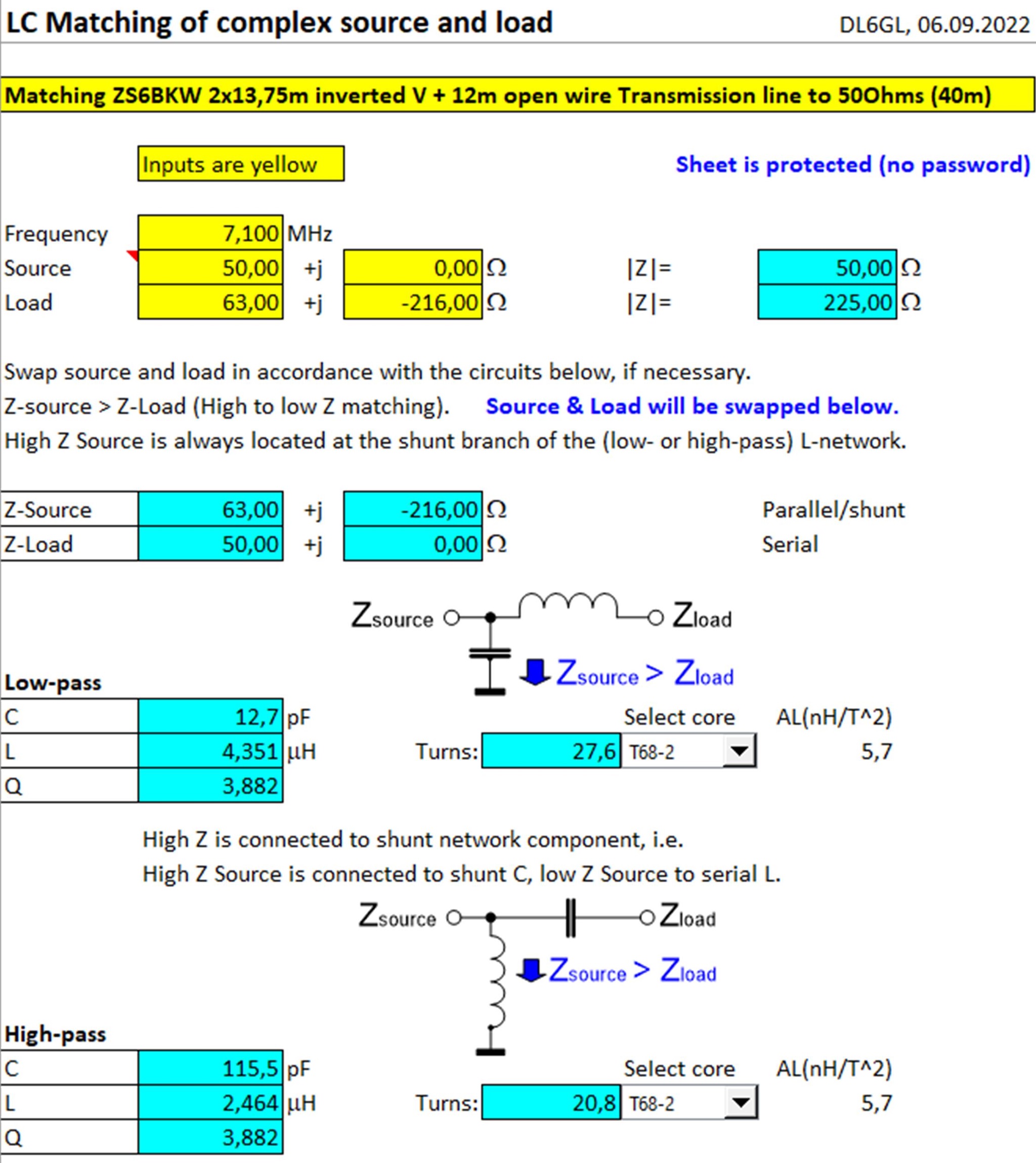
LC matching Excel calculation

Abb. 2.2: Beispielrechnung für komplexe Impedanzen mit Excel.

3 Anpassung mit Widerstandsnetzwerken

Auch mit Netzwerken aus ohmschen Widerständen sind Anpassungen von ZSource nach ZLoad möglich.
Bauformen: Pi- und T-Netzwerke. Im Gegensatz zu den o.g. LC-Netzwerken mit Transformation über Blindwiderstände sind sie naturgemäß nicht verlustlos.

Abb. 3.1: Pi- und T-Widerstandsabschwächer.

Anders als bei den L-Netzwerken ist auch ZSource = ZLoad möglich. Neben der beabsichtigten Signalabschwächung können solche R-Abschwächer z.B. eingesetzt werden, um einer Last, etwa einer Senderendstufe oder einem Filter, eine möglichst unbestechliche 50Ω-Eingangsimpedanz anzubieten, auch wenn die Quellimpedanz davon etwas abweichen sollte. Sie dämpfen zwar die Eingangsleistung, meist um hinnehmbare 3 bis 6dB, verhindern bzw. reduzieren dafür aber auch Reflexionen, mehr mit jedem dB.

R-Abschwächer sind anders als L-Netzwerke breitbandig, allerdings mit Leistungsverlusten.

4 Anpassung mit Transformatoren (Übertragern)

Für breitbandige und annähernd verlustlose Anpassungen bieten sich Transformatoren mit Ferritkernen an. Die Impedanzanpassung folgt dem Windungsverhältnis (Primärwicklung an Source, Sekundärwicklung an Load), "ideale" Transformatoren mit perfekter Kopplung der beiden Wicklungen und ohne Verluste im Kern und in den Wicklungen vorausgesetzt

Die Transformation kann mit den entsprechenden Windungsverhältnissen aufwärts (ZSource < ZLoad) oder abwärts (ZSource > ZLoad) erfolgen.

Die Auswahl der Windungen selber bei vorgegebenem Windungsverhältnis kann nicht willkürlich gewählt werden, z.B. "Sparversion" NPri = 1 Windung. Die Windungsimpedanzen sollten bei der minimal zu übertragenden Frequenz mindestens um den Faktor 4 größer sein als die Impedanzen der anzupassenden Module. Das Excel-Sheet markiert die Windungen für die vorgegebene Minimalfrequenz entsprechend rot oder grün.

Broadband transformer matching

Abb. 4.1: Transformatoranpassung.

Variationsmöglichkeiten neben den Windungszahlen sind mit der Auswahl der Transformatorkerns gegeben. Doppellochkerne haben neben dem höheren AL-Wert bei gleichem Kernmaterial, damit weniger Windungen, Vorteile geringerer magnetischer Streuverluste gegenüber Ringkernen. Das Ferritmaterial, bei Amidon z.B. Typ "77", "43", "61" in der Reihenfolge aufsteigender Frequenzbereiche, muss auch passen.

Für Impedanzanpassungen 1:4, z.B. 50Ω:200Ω, d.h. Windungsverhältnis 1:2, bieten sich bifilar gewickelte Autotrafos/Spartrafos (Anzapfung am Anfang der einen Wicklung und am Ende der anderen) an. Sie haben wegen der i.a. verdrillten Bifilarwicklung etwas geringere Verluste als Transformatoren mit getrennten Wicklungen. Kopplungsverluste i.a. wenige dB.

5 Anpassung mit angezapften Schwingkreisen

Ist eine frequenzselektive Anpassung über ein mehr oder weniger breites Frequenzband gewünscht, lassen sich auch Schwingkreise einsetzen. Dabei werden entweder die Kreisspule in einem bestimmten Anpassungsverhältnis angezapft oder der Kreiskondensator wird in einem entsprechenden Verhältnis in zwei Kondensatoren aufgeteilt ("tapped inductor" bzw. "tapped capacitor").

Abb. 5.1: Angezapfte Schwingkreise, links mit C, rechts mit L.

Eine Spulenanzapfung (rechts) ist i.d.R. aufwendiger herzustellen als die linke Variante mit 2 C's. Es sei denn, eine L = 1:2-Transformation, Z = 1:4, ist gewünscht. Dann wäre wieder wie im vorangegangenen Abschnitt eine einfach herzustellende bifilare Wicklung möglich. Hierzu sind die Wicklungsenden in Abb. 5.1 mit einem "•" gekennzeichnet.

Die Transformation erfolgt in beiden Darstellungen in Abb. 5.1 abwärts, also RS > RL.

Im Web ist oft als "Grundlage" zur Berechnung ein Simpelmodell zu finden (RS > RL), wobei L (Abb. 5.1 links) oder C (Abb. 5.1 rechts) anscheinend willkürlich vorgegeben werden können. Die Kreiskondensatoren (links) bzw. die Teilspulen (rechts) sind so zu bemessen, dass die Resonanzfrequenz der Anpassungsfrequenz entspricht.

Die Transformation RS/RL soll sich einfach aus dem Anzapfungsverhältnis berechnen lassen:

RS / RL = (C2 / Cges)² mit Cges = (C1*C2) / (C1+C2) bzw.
RS / RL = (Lges / L2)² mit Lges = L1+L2

Diese Näherung gilt allerdings nur für kleine L/C-Verhältnisse und damit geringen Belastungen von C2 bzw. L2 durch RL, was bisweilen unerwähnt bleibt.

In [7] hat Randy Evans, KJ6PO, den einfachen "Tapped Capacitor"-Ansatz untersucht und dabei mit Messungen festgestellt, dass er im Allgemeinen zu falschen Ergebnissen führt. Nur für recht kleine L/C-Verhältnisse kommt er der Wirklichkeit halbwegs nahe. Das unter [7] verfügbare Excel-Sheet von KJ6PO musste unbedingt einen Platz in meiner Sammlung finden.

Die von KJ6PO dargelegte recht aufwendige exakte Lösung ist im Download in den Grundzügen aufgezeigt. Beispiel im Excel-Sheet:

Tapped LC circuit

Abb. 5.2: Beispielrechnung für Tapped C-Resonanzkreis.

Das kleine LC-Verhältnis fällt hier auf, für geringere Bandbreiten noch deutlicher.

Excel ist ja nun unendlich geduldig beim Spielen mit möglichen Bauteilwerten. Test is best. In der Praxis wird es reichen, mit preiswerten LC-Metern ausgemessenen C's und L die Spule, etwa bei Luftspulen oder Ringkernen durch Dehnen oder Stauchen der Windungen, auf den Peak des Ausgangssignal (mit ansteigender und abfallender Flanke) an RL zu trimmen (= maximale Leistungsübertragung = Anpassung). Mit Schraubkernen in Zylinderspulen geht es noch einfacher.

6 Bridged Tee Diplexer

Etwas entfernter vom Thema der Anpassung verschiedener Impedanzen als die bisherigen Beispiele ist der Bridged Tee Diplexer. Er wird zum Beispiel eingesetzt, um Mischern über einen recht großen Frequenzbereich eine definierte konstante Lastimpedanz zu anzubieten. Das nachfolgende ZF-Filter, zumeist ein Quarzfilter, hat nur im Durchlassbereich die vorgegebene Systemimpedanz. Die abfallenden Filterflanken produzieren Reflexionen, die störend mit Verminderung der Intermodulationsfestigkeit auf den Mischer rückwirken. Auch alle weiteren Mischprodukte reflektiert ein Quarzfilter geradewegs zurück in den Mischer.

Bridged-Tee-Diplexer

Abb. 6.1: Bridged Tee Diplexer.

Die jeweils auf die Zwischenfrequenz abgestimmten LC-Kreise haben entgegengesetzte Aufgaben:

Der Serienschwingkreis Ls / Cs stellt bei der Resonanzfrequenz = ZF-Mittenfrequenz einen ungehinderten Durchgang dar. Im Durchlassbereich des ZF-Filters mit Nominalimpedanz ist damit der Mischer korrekt abgeschlossen. Abseits davon, schon an den Filterflanken, aber nicht mehr.
Der Parallelschwingkreis Lp / Cp ist bei Resonanzfrequenz hochohmig und macht damit den unteren Ast in Abb. 6.1 unwirksam. Weiter ab von der Resonanzfrequenz bildet er über die beiden Serienwiderstände R zunehmend einen sauberen Abschluss Zin = Zout = R.

Vereinfacht gesagt: Der Serienkreis bildet für die ZF-Mittenfrequenz einen Kurzschluss, der Parallelkreis sperrt. Abseits davon bildet der Parallelkreis einen Kurzschluss an die beiden Widerstände R = Zin, der Serienkreis sperrt. Der Diplexer wirkt als Bandpass.

Oft ist der Diplexer mit identischen Serien- und Parallelkreisen in der Literatur zu finden. Nachteil ist die große Bandbreite im Vergleich zur Bandbreite eines ZF-Quarzfilters. Mit Vergrößern des LC-Verhältnisses im Serienkreis und entsprechendem Verkleinern im Parallelkreis kann jedoch die Bandbreite angepasst werden. Das Excel-Sheet im Download ermöglicht eine Auslegung für Kreisgüten Q von 1 bis 10, wobei sinnvolle Anwendungen eher im Bereich bis maximal 5 liegen werden.

Bridged Tee Diplexer calculation