2 Tandem match-Koppler
Erstellt: DL6GL, 04.03.2017, letzte Änderung 23.04.2021
| « 1 Lösungsansätze | TOP | » 3 Logarithmische Verstärker |
Wie beim vorherigen Diodenkonzept bilden der eigentliche Koppler und die logarithmischen Verstärker eine Einheit. Die Kopplerbauart und die Log Amps richten sich nach dem gewünschten Frequenzbereich, für HF etwa der Tandem match- (Stockton-) Koppler und AD8307, die wir nachfolgend darstellen.
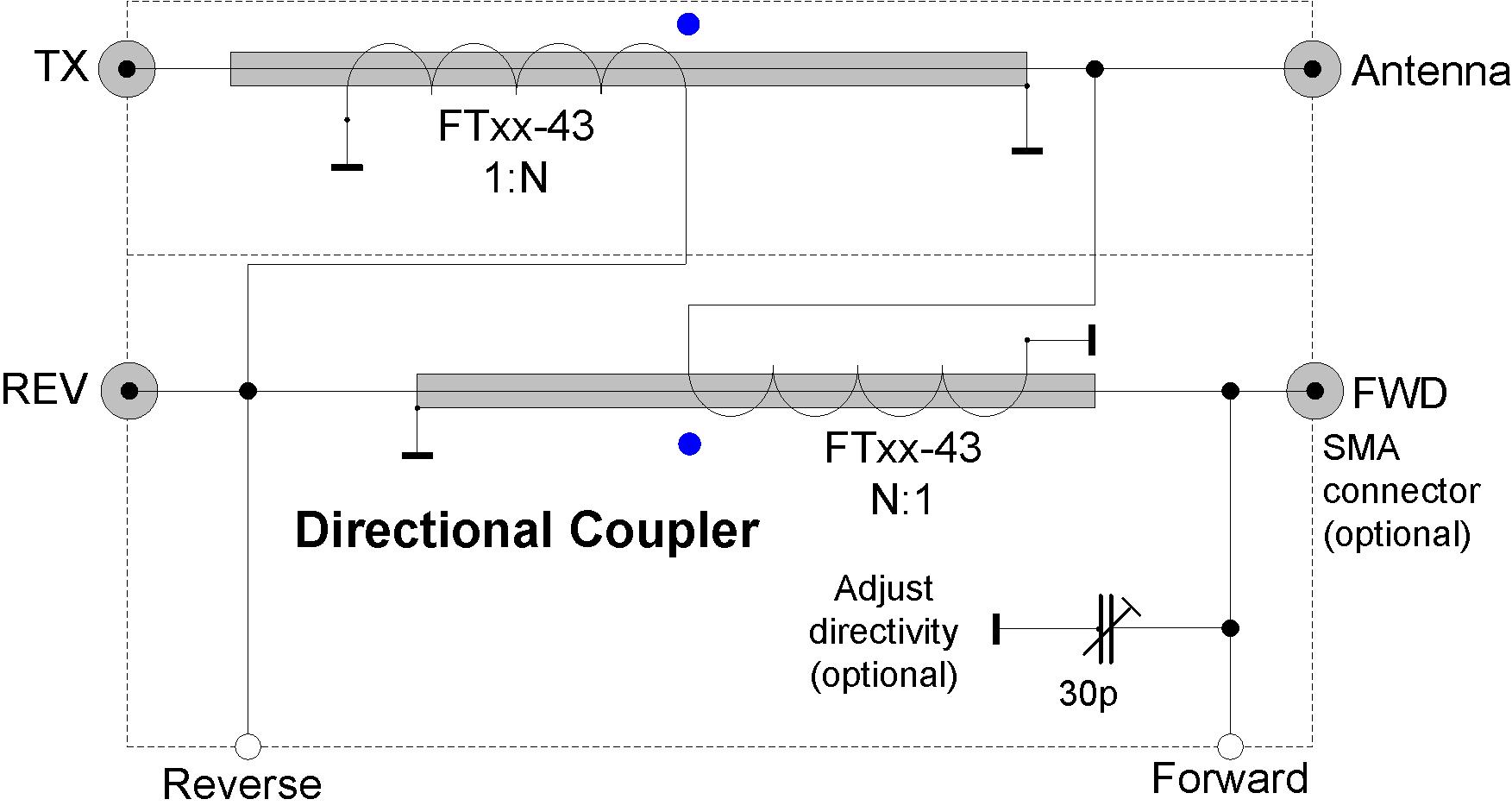
Abb. 2.1: Tandem match Koppler, Realisierung.
Je nach Polung der Transformatoren vertauschen die FWD- und REV-Ports. Die hier verwendete Polung ergab kürzere Verbindungen. Die blauen Punkte in Abb. 2.1 entsprechen den weißen Anschlüssen in Abb. 2.3. Hier ist der Forward-Port auf der Seite des Antennenausgangs. Zur Polung der Transformatoren siehe auch hier aus dem ersten Vorläufer mit Diodengleichrichter. Näheres zu Messungen an Richtkopplern ist hier aus einem früheren Artikel zu finden. Siehe aber auch hier (neuerer Artikel).
Die für den Betrieb erforderlichen 50Ω-Abschlusswiderstände an den Forward- und Reverse-Ports bilden sauber abgeschlossene Pi-Abschwächer auf der Auswerteplatine (Abb. 3.1).
Wer den Koppler vorher mit einem Netzwerkanalysator vermessen will, sollte das untere Koax-Kabel in Abb. 2.1 auch an HF-taugliche Buchsen nach außen führen und die Abschlusswiderstände wechselseitig für die Messung dort aufstecken. Mit dem Trimmer lässt sich die Richtschärfe noch deutlich verbessern. Das geht aber auch ohne Netzwerkanalysator, wie wir unten zeigen.
Der Tandem match-Koppler, landläufig - zu Unrecht - nach dem von David Stockton, G4ZNQ, in Sprat 1989/90 veröffentlichten Bi-directional Inline Wattmeter [3] benannt, geht auf das Patent von Carl G. Sontheimer und Raymond E. Frederick [4] aus dem Jahr 1969 zurück. Vor David Stockton hat ihn John Grebenkemper, KI6WX, in QST, Jan 1987, in Amateurkreisen bekannt gemacht.
Die Arbeitsweise soll am folgenden Prinzipschaltbild mit geläufigerer umgedrehter Polung des Stromtransformators wie bei K6JCA erklärt werden.
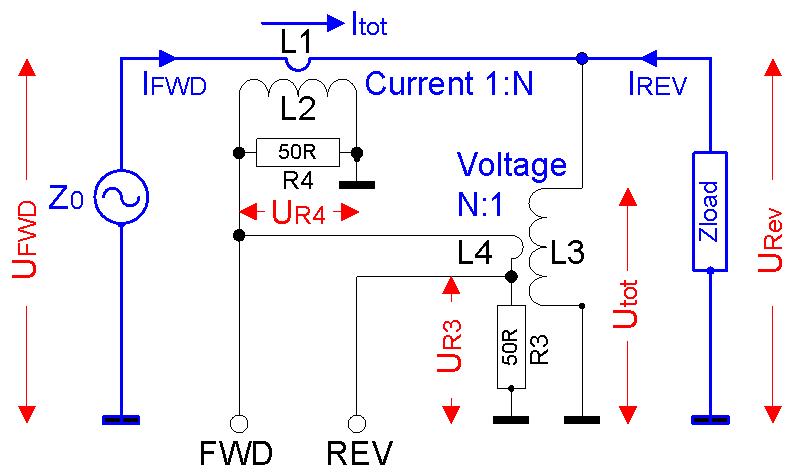
Abb. 2.2: Tandem match Koppler, Prinzipschaltbild.
Wir folgen dabei den großartigen Ausführungen von Jeff C. Anderson, K6JCA, in [1]. Die praktische Berechnung haben wir mit Excel nachvollzogen. Dabei kam u.a. heraus, dass die Auslegung der Ringkerne in unseren o.g. ersten Versuchen etwas blauäugig war. Auch alte Knaben können mit der Zeit noch ein wenig klüger werden.
Den vom TX zur Last (von links nach rechts) und den ggf. von der Last (von rechts nach links) reflektierten Strom, IFWD bzw IREV, misst der obere 1:N-Transformator, die entsprechenden Spannungen der rechte N:1-Transformator. "FWD" = Forward, "REV" = Reverse (Reflected). Beide Transformatoren arbeiten auf je einen 50Ω-Lastwiderstand R3 und R4, entsprechend der Systemimpedanz Z0. Reflexionen und damit nennenswerte "REV"- Ströme und -Spannungen treten dann auf, wenn die Last Zload von der Systemimpedanz Z0 abweicht.
K6JCA erklärt in [2] so umfassend die Herleitung der Strom- und Spannungsverhältnisse im Koppler, dass wir das nur schlechter machen könnten. Hier also sogleich die Ergebnisse:
Der Spannungsabfall über der Primärwicklung L1 des Stromtransformators ist vernachlässigbar. Damit sind die Spannungen über der Last Zload, die vom TX gelieferte Spannung am Eingangsport und die an der Primärwicklung des Spannungstransformators L3 identisch. Der Strom durch L1 ist damit
I = U / Zload.
Der Strom durch die Sekundärwicklung L2 des Stromtransformators ist dann I / N und die in die Sekundärwicklung L4 des Spannungstransformators induzierte Spannung ist U / N.
Nach einigen Umformungen ergibt sich
UR4 = -UR3 * (Zload - R4) / (Zload + R3)
Mit R3 = R4 = Z0 = 50Ω zeigt sich, dass der blau markierte Term nichts anderes ist als der Reflexionskoeffizient Γ (Gamma)
(Zload - Z0) / (Zload + Zo) = Γ
Also: -UR4 / UR3 = Γ (Reflexionskoeffizient)
UR4 und UR3 stehen an den Ports "FWD" und "REV" zur Verfügung. Damit ergibt sich das Stehwellenverhältnis zu
SWR = (1 + | Γ |) / (1 - | Γ |)
Der Betrag des wegen des i.a. komplexen Lastwiderstands Zload komplexen Reflexionskoeffizienzen Γ wird landläufig mit ρ (rho) bezeichnet.
Wie K6JCA in [1] - Part 5 Directional Coupler Design - ausführlich darlegt, ist bei der Auslegung der Strom- und Spannungstransformatoren einiges zu beachten. Abhängig von der TX-Leistung, der Windungszahl und den Kerneigenschaften gilt es, eine übermäßige Erwärmung bis hin zu einer möglichen Sättigung infolge einer zu hohen magnetischen Flussdichte in den Kernen zu vermeiden. Kritisch ist der Spannungstransformator. Den beschriebenen Rechengang haben wir in einem Excel-Sheet nachgebildet (mit einer Zusammenstellung der verwendeten Formeln im Download).
Kernaussagen aus den Berechnungen und den Messungen an unserem 50W-Prototyp:
- Die Impedanz des Spannungstransformators muss bei der niedrigsten Nutzfrequenz mindestens 10*Z0 = 500Ω betragen, damit sie keine zusätzliche Last bildet.
- Die magnetische Flussdichte sollte zur Vermeidung einer übermäßigen Erwärmung bestimmte frequenzabhängige Grenzwerte nicht überschreiten. Daten und Berechnungsformel für Amidon FT-Ringkerne im Excel-Sheet im Download. Kritisch ist hier der Spannungstransformator.
- Strom- und Spannungstransformator können mit unterschiedlich großen Ringkernen ausgelegt werden, Spannungstransformator, ggf. gestockt, tendenziell größer als der Stromtransformator. Aber identische Windungszahlen, d.h. Kopplungsfaktoren.
Soweit wir das überblicken, hat es eine vergleichbare Berechnung im Web noch nicht gegeben. Thanks a lot, Jeff, great!
Hier noch eine Übersicht möglicher Kopplerkonfigurationen mit der Maßgabe
- maximale magnetische Flussdichte im Spannungstransformator ~80 Gauss bei Minimalfrequenz 3,5MHz (mit 1,8MHz nicht mehr erfüllt) für geringe Wärmeentwicklung,
- dabei kleinst mögliche Ringkerne.
| PEP | W | 10 | 20 | 50 | 100 | 200 | 750 |
| Stromkern | FT50-43 | FT50-43 | FT50-43 | FT50-43 | FT50-43 | FT50-43 | |
| Spannungskern | FT50-43 | FT50-43 | 2xFT50-43 | FT114-43 | FT114-43 | FT140-43 | |
| Windungen | 20 | 27 | 23 | 24 | 30 | 29 | |
| Kopplungsfaktor | dB | -26,0 | -28,6 | -27,2 | -27,6 | -29,5 | -29,3 |
| Spannungstransformator | |||||||
| Min. XL @ 3.5MHz | Ω | 3.870 | 7.054 | 10.237 | 7.638 | 11.935 | 2.589 |
| B-Max @ 3.5MHz | Gauss | 83 | 87 | 81 | 76 | 86 | 80 |
Tab. 2.1: Mögliche Strom- und Spannungskoppler-Konfigurationen.
Die magnetische Flussdichte im Stromtransformator von maximal 8,6Gauss im 750W-Koppler erlaubt immer noch den Einsatz eines kleinen FT50-43-Ringkerns, wenn er denn noch auf das einzusetzende Koaxkabel passt. Da könnte man schon mal Platz und Geld sparen.
Bevor es ans Bauen wie im nachfolgenden Bild geht, lässt sich mit dem Excel-Sheet im Download trefflich spielen, um für die vorgesehene maximale TX-Leistung die passenden Ringkerne, Kopplungsfaktoren ( d.h. Windungszahlen) und die Dimensionierung der Abschwächer vor den Log-Amps herauszufinden.
- Die Windungszahl n bestimmt die ausgekoppelte HF-Leistung.
Der Kopplungsfaktor CF = 20*LOG(n) ist der ausgekoppelte Anteil, genauer das logarithmische Verhältnis der primären zur ausgekoppelten Leistung in dB,
d.h. ein hoher CF (hohe Windungszahl) koppelt wenig HF aus. Für den Kurzwellenbereich sollte n~30 das Maximum sein. - Die Windungszahl bestimmt wiederum die über den Stromtransformator in die Antennenleitung hinein transformierte Leitungsimpedanz Z = R /n^2, R= Systemimpedanz 50Ω, d.h. eine höhere Windungszahl bewirkt eine geringere Einfügedämpfung des Kopplers.
- Eine höhere Windungszahl ergibt eine niedrigere magnetische Flussdichte im Spannungstransformator bei vorgegebener TX-Leistung. Zusammen mit der zu verwendenden Ringkerngröße ist die vom Spannungstransformator zu verkraftende magnetische Flussdichte, abhängig von dem maximal auftretenden VSWR, zu begrenzen. Platz sparend wäre ein Stocken mehrerer Ringkerne im Spannungstransformator falls nötig.
- Der Kopplungsfaktor bestimmt die Größe der Abschwächer vor den Log Amps und damit die Belastung der verwendeten Widerstände. Ein hoher Kopplungsfaktor macht eine geringere Abschwächung notwendig, in der Folge geringere Anforderungen an die Belastbarkeit der im Log Amp-Modul verwendeten SMD-Widerstände der Größe 0805, siehe Abschnitt 3.

Abb. 2.3: Musteraufbau der 50W-Variante von DG1KPN.
Der untere Spannungstransformator wird gegen den oberen Stromtransformator um 180° gedreht auf das Koaxkabel aufgesetzt, siehe blaue Polaritätspunkte in Abb. 2.1, hier weiß.
| « 1 Lösungsansätze | TOP | » 3 Logarithmische Verstärker |