Bode-Plots mit Excel darstellen und berechnen
Erstellt, DL6GL, 29.07.2023, letzte Änderung 13.08.2023
Gemessene Frequenzgänge als Bode-Plot mit MS Excel darzustellen, ist zwar nicht allzu kompliziert, erfordert aber doch etwas Handarbeit. Ohne Übung kann es mühsam werden, diverse Einstellungsfenster abzuarbeiten. Mit Excel VBA wurde das vor ein paar Jahren automatisiert.
Diese Vorlage wartete auf eine Ergänzung. Zumindest einfache Filterschaltungen wie Hoch- oder Tiefpässe sollten mit vergleichsweise wenig Aufwand, ohne Butterworth- oder Chebychev-Polynome, berechenbar sein, etwa ein RC-Glied im Audiobereich an einem OpAmp. Ja, es gibt Programme und Online-Rechner für solche Aufgaben. Wie das mit Excel geht, wollte ich dann doch mal wissen.
Die dabei entstandene Excel-Arbeitsmappe bietet zwei Alternativen:
- Ist nur eine Messreihe mit einer oder auch zwei Variablen gegen die Frequenz in einem Bode-Plot darzustellen, wird diese in der Datentabelle (Abb. 2) erfasst.
Mit Festlegung der Frequenzeinheit (Hz, kHz, MHz) und Klick auf "Show Chart", Abb. 1, wird der Plot automatisch formatiert angezeigt. - Eingabe der Bauteiledaten von R, L, C (Abb. 1) und der Berechnungsformeln (Abb. 2) zur Modellierung der zu berechnenden RLC-Schaltung. Abschließend Klick auf "Show Chart".
Die Frequenzachse kann linear oder logarithmisch skaliert werden.
Viele einfache RLC-Kombinationen wie Hoch- oder Tiefpässe sind als Spannungsteiler aufgebaut. Einen Spannungsteiler aus zwei Widerständen zu berechnen gehört zum täglichen Handwerk. Die Hinzunahme eines induktiven oder kapazitiven Widerstandes ist auch kein Hexenwerk, wenn einige Grundregeln beim Rechnen mit komplexen Zahlen beachtet werden. Im Download werden einige Berechnungsbeispiele einschließlich der Realisierung mit Excel gezeigt.

Abb. 1: Eingabeteil des Excel-Sheets für einen LC-Tiefpass mit Serien- und Lastwiderstand.
Das Rechenmodell für Übertragungsfunktion und Phase ist in einer Datentabelle hinterlegt.
Einige Formeln zu diesem Tiefpass in RLC-Circuits_005 waren falsch. In RLC-Ciruits_006 korrigiert.
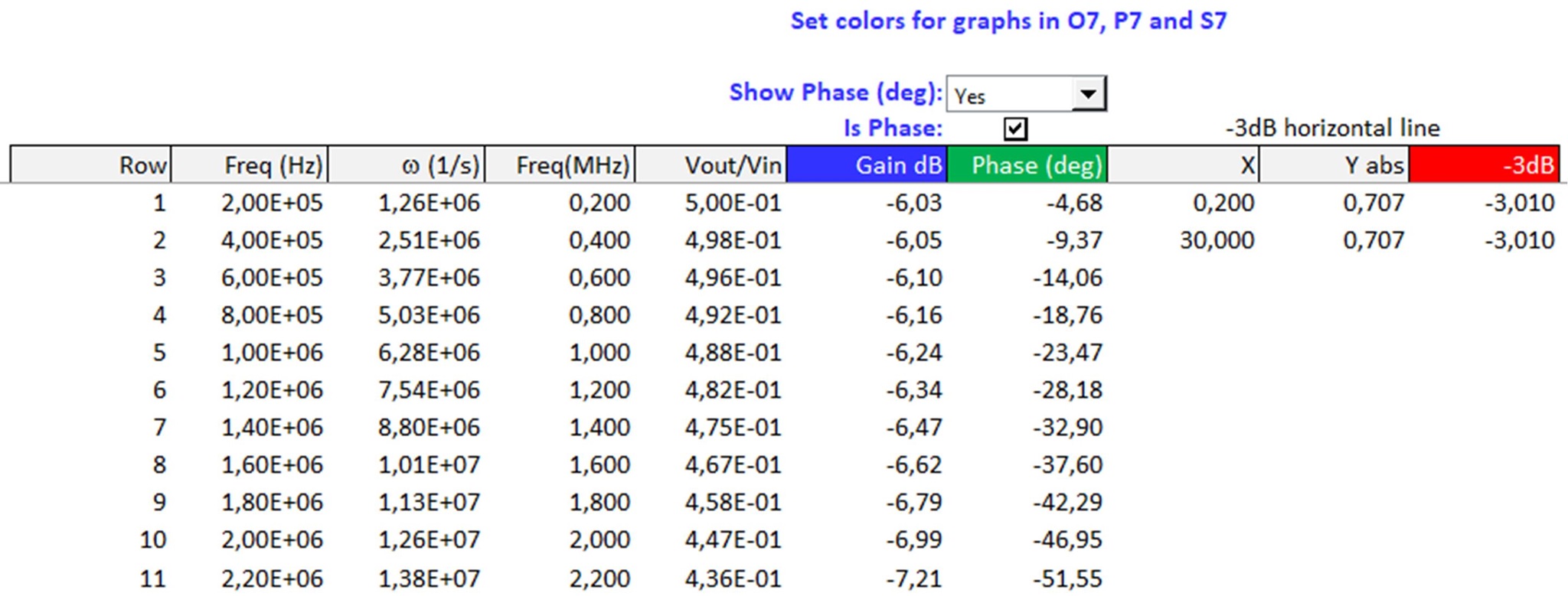
Abb. 2: Datentabelle: Frequenz, Vout/Vin (absolut), Gain (dB), Phase und -3dB-Linie.
Die Beschriftungen in den farbig hinterlegten Kopfzeilen und deren Hintergrundfarbe können angepasst werden. Sie erscheinen in der Grafik als Legenden. Die Hintergrundfarben legen die Linienfarben fest.
Nach Klick auf "Show Chart" (Abb. 1) wird der Bode-Plot aus den Daten automatisch erstellt.
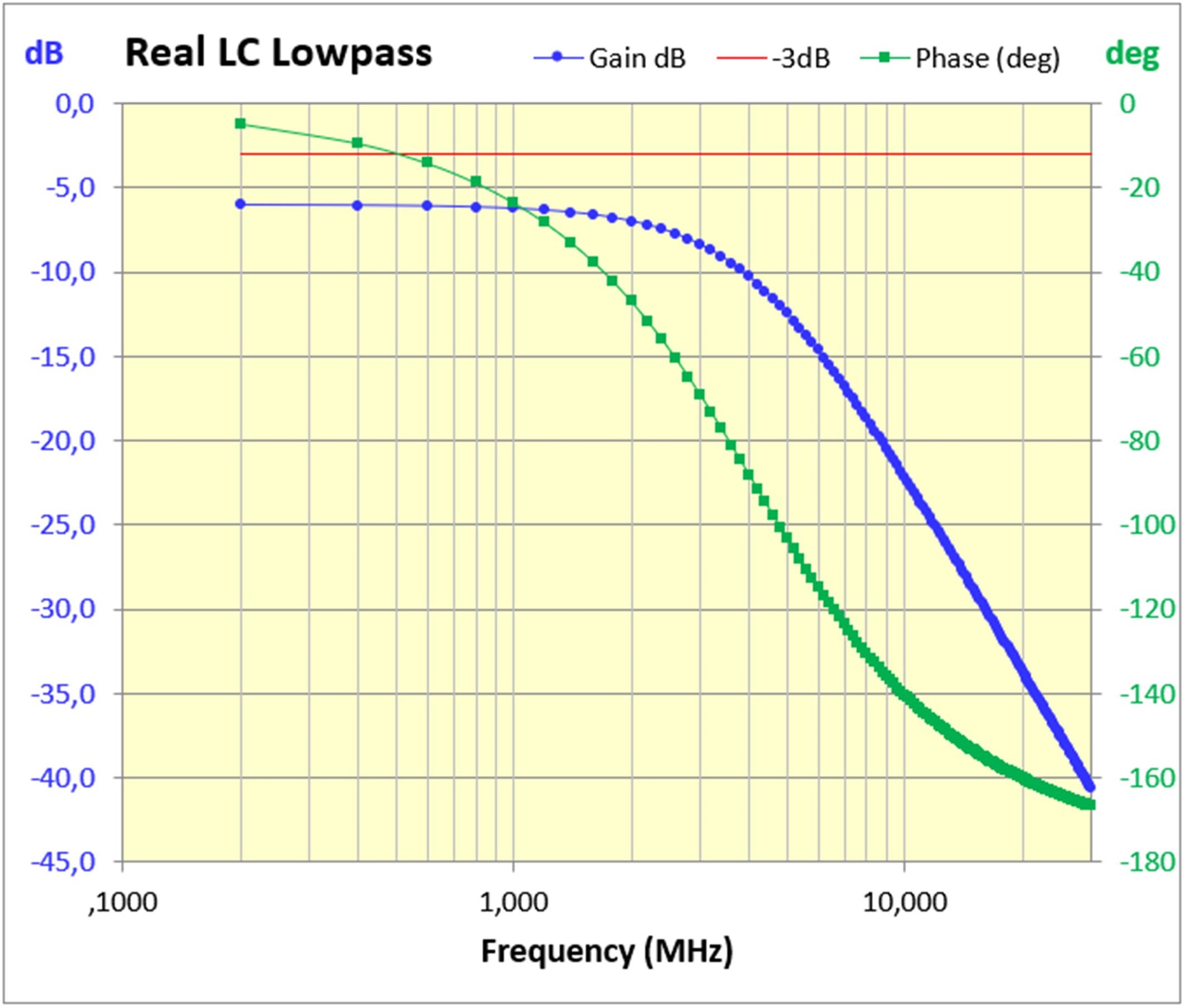
Abb. 3: Bode-Plot zum o.a. LC-Tiefpass.
13.08.2023: Update RLC-Circuits_006.xlsm. Bei der Erweiterung des ursprünglichen Programms zur Darstellung von Bode-Plots auf die Darstellung auch von Phasen habe ich einiges verbogen. Nun sollte es passen.
Download
Bode-Plots darstellen und berechnen.pdf