Verlustlose Standard LC-Filter
Erstellt: DL6GL, 31.08.2023, letzte Änderung 04.12.2023
Der Artikel über Bode-Plots musste notgedrungen zu dem Schluss kommen, dass die dort gezeigte Art, auch nur einen einfachen RLC-Tiefpass zu berechnen, ihre Grenzen hat. Das hat mich neugierig auf "mehr" gemacht. Eine wirkliche Notwendigkeit dazu gab es nicht, waren doch die Eingangsbandpässe und die PA-Tiefpässe in meinem TRX vor vielen Jahren berechnet, gebaut, gemessen und bestätigt.
Nun ja, dazu habe ich damals nach anfänglichen frustierenden Versuchen, so etwas per Hand zu berechnen, das Programm Elsie benutzt. Egal, interessieren würde es mich schon, wie das eigentlich funktioniert und warum.
Das Internet ist voll von meist komplizierten Abhandlungen über Filtertheorien, zumeist für Mikrowellenanwendungen. Hier will ich versuchen, die dahinter liegenden Grundzüge aufzuzeigen, soweit sie meinem Verständnis zugänglich waren. Als Amateur muss man sich ja nicht in jede Feinheit vertiefen, auch wenn dann manch ein Zusammenhang und manche Formel als gegeben hinzunehmen ist.
Herausgekommen ist eine aus Expertensicht wohl eher oberflächliche Betrachtung der Zusammenhänge als erklärender Text und dessen praktische Umsetzung mit MS Excel. Beides im Download. Um es noch mit diesen bescheidenen Ansätzen überschaubar zu halten, werden nur verlustlose passive LC-Filter mit den gängigen Näherungen nach Butterworth und Chebyshev betrachtet:
- Hoch- und Tiefpass,
- Bandpass und Bandsperre.
Zwei Beispiele werden nachfolgend gezeigt.
Die Berücksichtigung der Verluste in realen L's und C's wäre noch einmal eine besondere Herausforderung,
die ich im Nachgang zu diesem Artikel aufgegriffen habe; siehe Hinweis ganz unten auf dieser Seite.
Butterworth Tiefpass
Die Struktur der Excel-Sheets ist an die o.g. Bode-Plot-Sheets angelehnt, aus denen sie entstanden sind. Zunächst die Grundlage aller Berechnungen, sowohl für die Butterworth- als auch für die Chebyshev-Näherung: die Tiefpass Prototyp-Elementwerte gk:
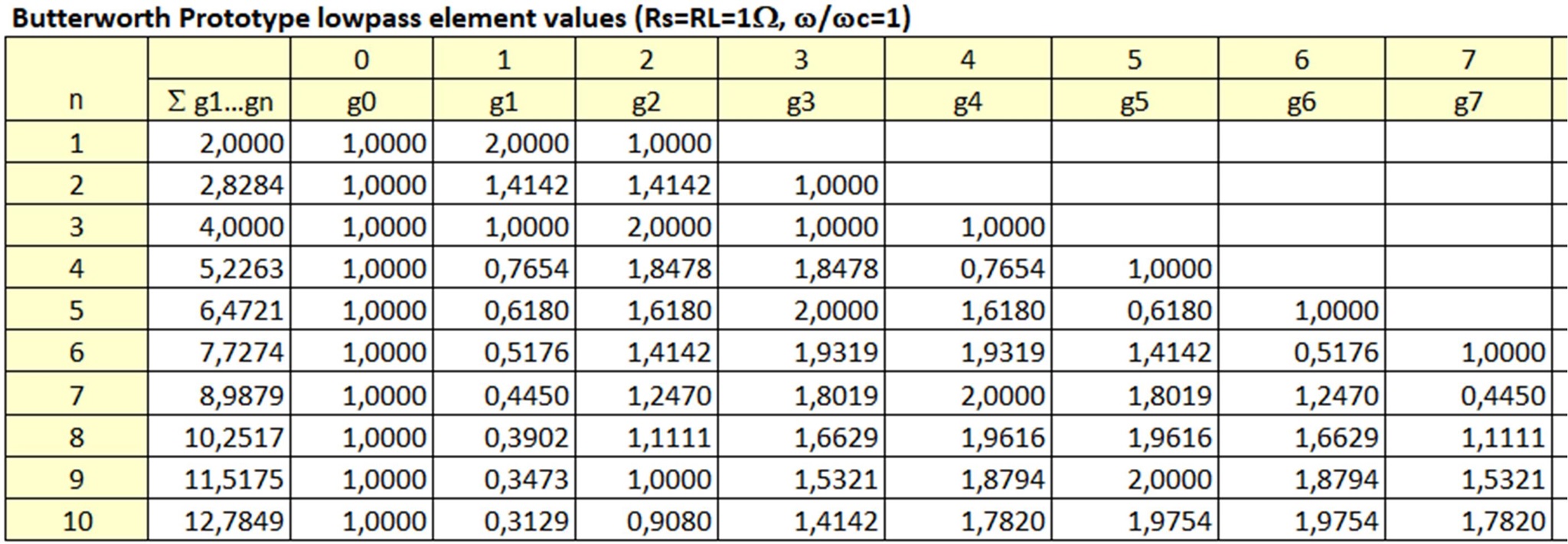
Abb. 1: Butterworth Tiefpass Prototyp-Elementwerte gk.
Aus diesen Tiefpass Prototyp-Elementen lassen sich alle anderen LC-Filter – Hochpass, Bandpass und Bandsperre – mit einfachen Faktoren transformieren und auf die gewünschten Frequenzen und Impedanzen skalieren.
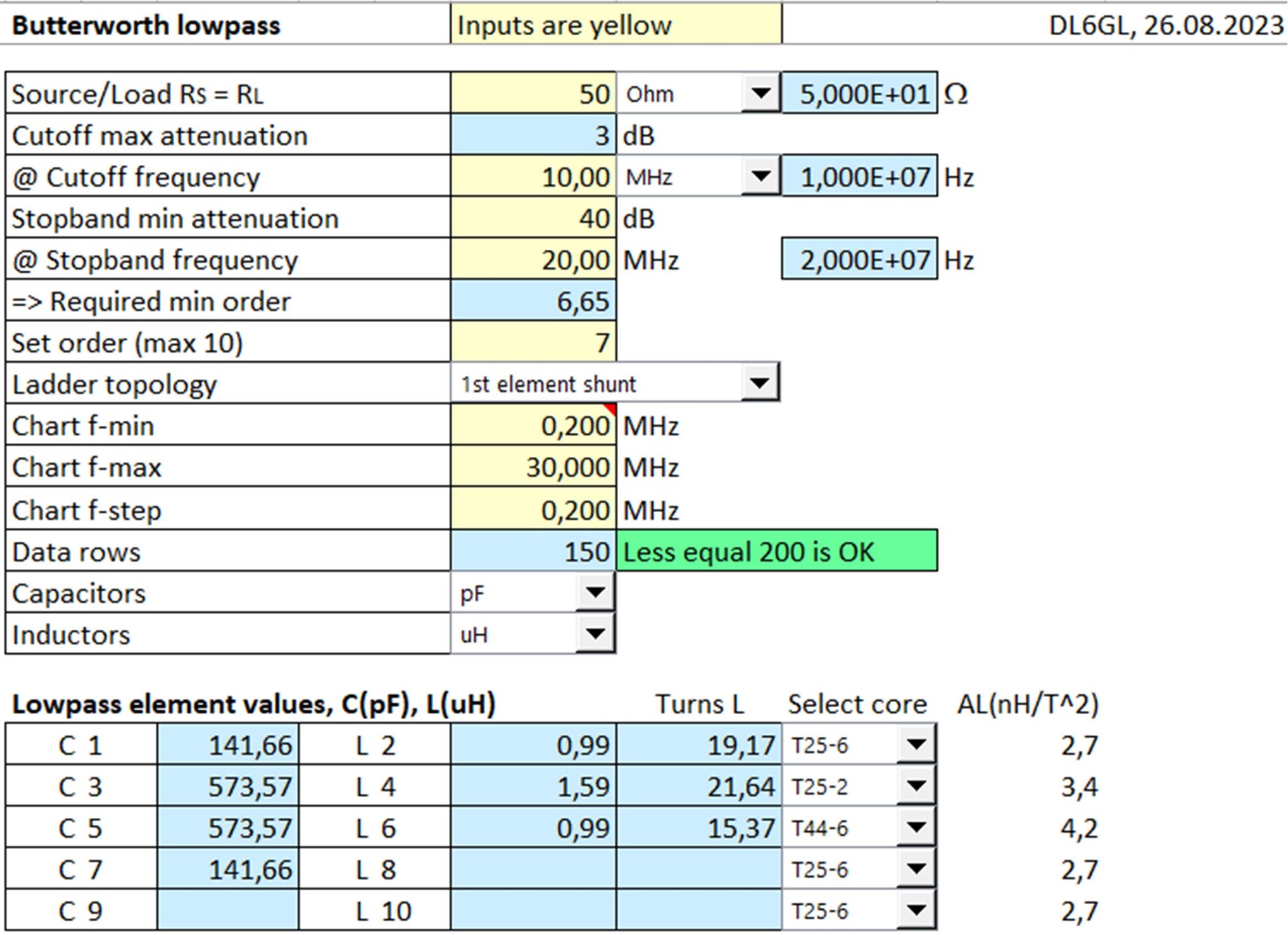
Abb. 2: Eingabefelder für einen Butterworth-Tiefpass und berechnete L-/C-Komponenten.
Bis hierher werden alle Berechnungen einschl. der Datentabelle für die Bode-Plots für Insertion Loss und Return Loss mit Excel-Bordmitteln vorgenommen, so dass auch freie Programme wie LibreOffice Calc verwendet werden können sollten. Alleine die automatische Erstellung des Bode-Plots erfolgt per Excel VBA. Bei Excel müssen dazu die Makros aktiviert werden. Der VBA-Code ist offen einsehbar.
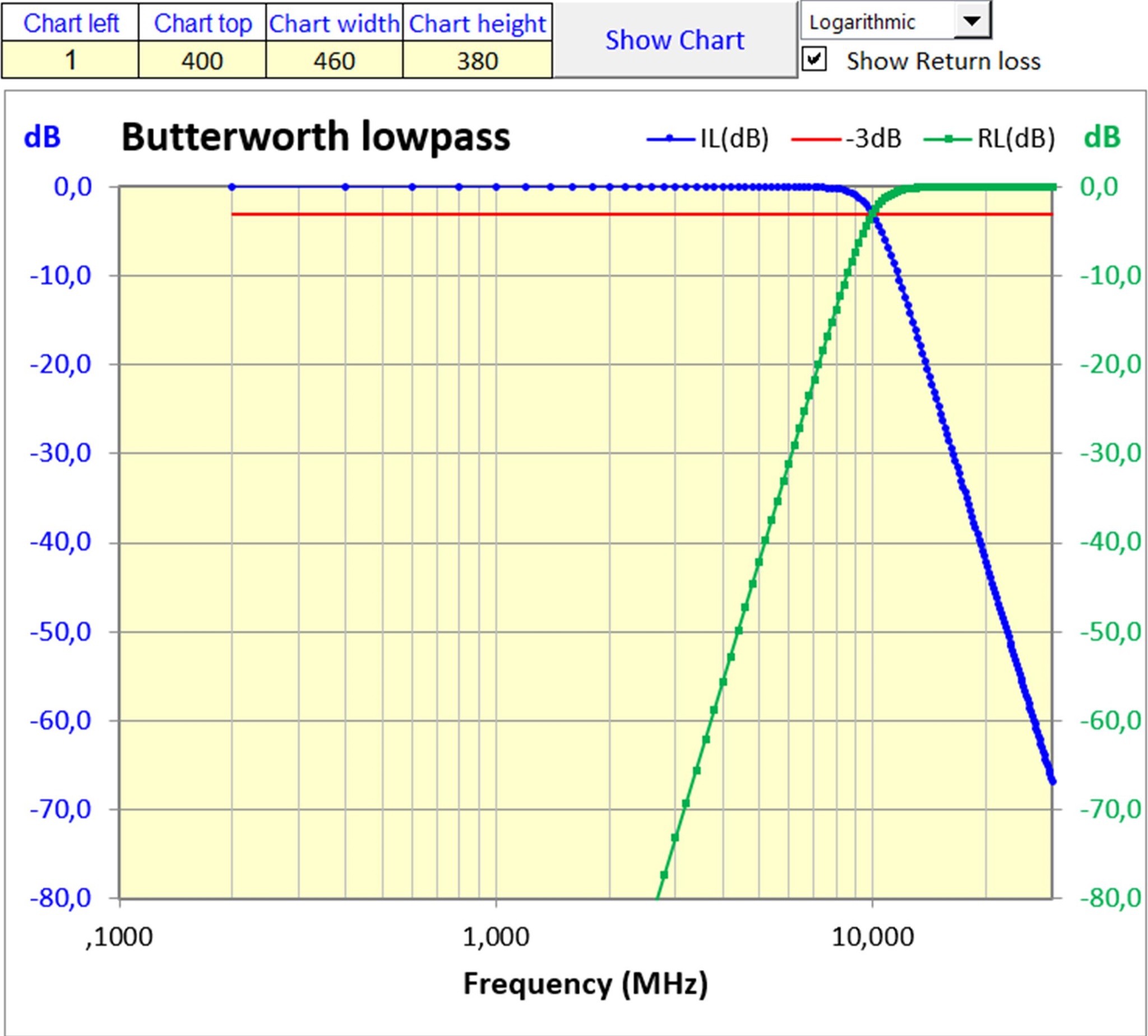
Abb. 3: Butterworth-Tiefpass, Bode-Plot für Insertion- und Return Loss.
Chebyshev Bandpass
Die Eingabe und Darstellung der berechneten L- und C-Komponenten für die anderen Filter – Hochpass, Bandpass und Bandsperre – ist vergleichbar mit Abb. 2. Das Ergebnis für ein Chebyshev-Bandfilter sieht dann etwa so aus:
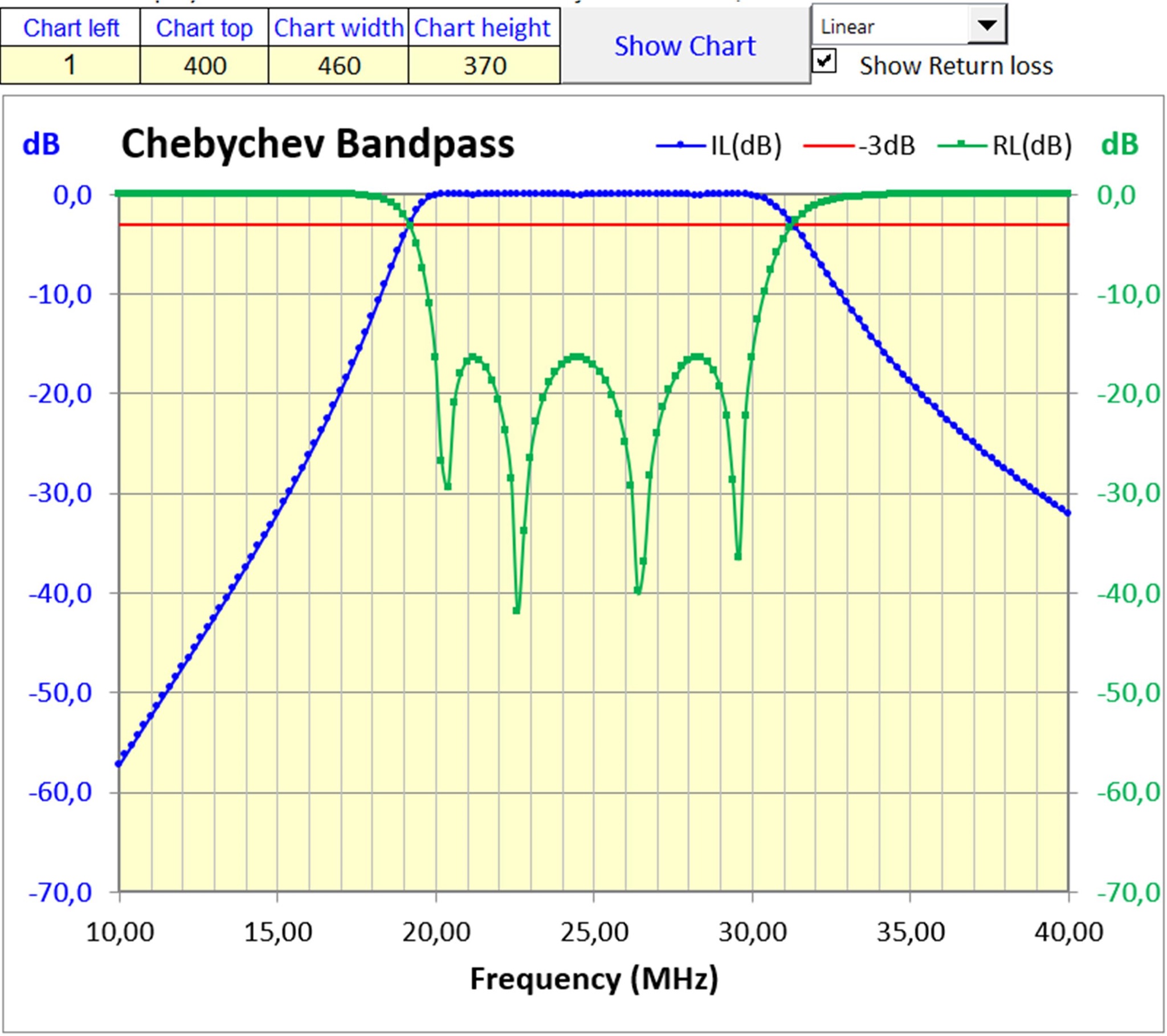
Abb. 4: Chebyshev-Bandpass, Bode-Plot für Insertion- und Return Loss.
Sowohl die berechneten Werte für die L- und C-Komponenten als auch die Bode-Plots wurden mit Elsie verglichen. Das passte. In Elsie wurden dazu die Güten von L und C hochgesetzt, um die Plots vergleichbar zu machen. Nachteil der vereinfachten Berechnung hier mit verlustlosen Komponenten ist, dass die Auswirkung auf die Dämpfung insbes. der Spulenverluste und verschiedener Bandbreiten nicht beurteilt werden kann. Die Bestätigung bleibt, dass mit den Möglichkeiten eines Tabellenkalkulationsprogramms wie MS Excel auch solche Filter berechenbar sind.
Detaildarstellung zur Auslegung von Butterworth- und Chebyshev-Filtern und die zugehörigen Berechnungen mit MS Excel sind im Download zu finden.
Ein weiteres Manko zeigen die aus der rechnerisch einfachen Transformation des Tiefpass-Prototyps in die konventionellen Bandpässe aus Parallel- und Serien-LC-Kreisen auf. In der Amateurpraxis zumeist eher schmale Bandfilter mit relativen Bandbreiten um 10% und weniger sind mit entweder sehr kleinen oder sehr großen Kapazitäten oder Induktivitäten nicht vernünftig realisierbar. Das dargelegte einfache Modell der Butterworth- und Chebyshev-Prototypen erschöpft sich hier. Eine Verfeinerung mit Schmalband-Näherungen (Narrow Band Approximation) durch weitere Transformationen der o.a. Parallel- oder Serien-LC-Kreise wäre vonnöten.
LC-Filter mit verlustbehafteten Komponenten
22.10.2023: Ich hab's gewagt und es hat hingehauen: Seite Bandfilter berechnen mit realen Komponenten.
- Konventionelle Bandfilter wie oben,
- spezielle für kleine relative Bandbreiten, wie sie tatsächlich für die Amateurfunkbänder gebraucht werden,
wahlweise Impedanzskalierung zur Optimierung von LC-Verhältnissen, - Hoch- und Tiefpässe: Butterworth, Chebyshev und Cauer,
- alle mit Berücksichtigung der Spulen- und Kondensator-Verluste / -Güten.
- Auslegung der Komponenten, Berechnung und Plot von
- Durchgangsdämpfung, Insertion loss,
- Reflexionsdämpfung, Return loss,
- Eingangsimpedanz, Input impedance,
- Stehwellenverhältnis, VSWR.
- Berechnung und und Plot der o.g. Größen aus willkürlich einzugebenden Filterkomponenten, etwa aus Baubeschreibungen ohne entsprechende Visualisierungen oder Messungen.
Downloads